Definizione di segmento, segmenti consecutivi ed adiacenti
I segmenti sono uno dei concetti fondamentali in geometria e costituiscono la base per comprendere figure più complesse e per risolvere problemi geometrici.
In questa pagina, esploreremo in dettaglio la definizione di segmento, i segmenti consecutivi e i segmenti adiacenti, illustrandone le proprietà e fornendo esempi pratici per chiarire il loro utilizzo.
Definizione di segmento
Un segmento è una parte di una retta delimitata da due punti distinti, chiamati estremi. Se A e B sono i due estremi, il segmento è indicato come AB. A differenza di una retta, che si estende indefinitamente in entrambe le direzioni, un segmento ha una lunghezza finita determinata dalla distanza tra i suoi estremi.
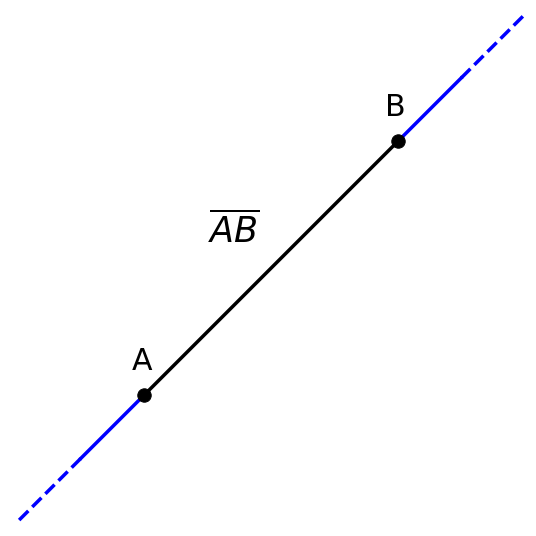
Proprietà di un segmento:
Lunghezza: la lunghezza di un segmento AB è la distanza tra i punti A e B.
Punti Interni: tutti i punti che si trovano tra A e B sono considerati punti interni del segmento.
Un segmento può essere rappresentato graficamente come una linea retta che collega due punti distinti. In notazione, il segmento con estremi A e B si indica come AB.
Segmenti consecutivi
I segmenti consecutivi sono segmenti che condividono un estremo comune. In altre parole, se abbiamo due segmenti AB e BC, questi segmenti sono consecutivi se condividono il punto B.
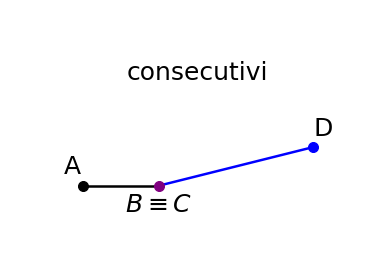
Proprietà dei segmenti consecutivi:
Estremo comune: due segmenti consecutivi condividono un solo punto, detto estremo comune.
Formano una poligonale: i segmenti consecutivi possono essere concatenati per formare una poligonale, una figura composta da segmenti collegati tra loro, ma che non appartengono alla stessa retta.
Segmenti adiacenti
I segmenti adiacenti sono segmenti che non solo condividono un estremo comune, ma si trovano anche sulla stessa retta. Questo implica che i segmenti adiacenti sono parte di una stessa linea continua senza interruzioni. Se abbiamo i segmenti AB e BC, essi sono adiacenti se A, B, C appartengono alla stessa retta e se i due segmenti AB e BC sono consecutivi.
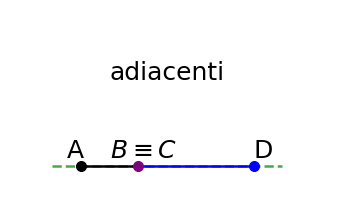
Proprietà dei segmenti adiacenti:
Estremo comune: condividono un estremo.
Unione: la lunghezza del segmento risultante dall'unione di due segmenti adiacenti AB e BC è la somma delle lunghezze dei segmenti originali AC.
Conclusione
I segmenti sono elementi fondamentali della geometria che ci aiutano a comprendere e descrivere lo spazio bidimensionale. La definizione di segmento, insieme alla comprensione dei segmenti consecutivi e adiacenti, fornisce una base solida per lo studio di figure geometriche più complesse.