Geometria euclidea piana: enti e postulati
La geometria euclidea piana, o semplicemente geometria piana, è un sistema matematico, appartenente alla Geometria, che studia enti e figure piane, cioè in 2 dimensioni: alcuni esempi possono essere la retta, l’area di un poligono, un angolo compreso fra due segmenti, eccetera.
L’introduzione di questa branca della Geometria è attribuita al matematico Euclide, che ne diede una formulazione sistematica nella sua opera "Elementi". Il punto di partenza della sua geometria sono cinque concetti intuitivi detti postulati, o assiomi, da cui si possono dedurre logicamente tutti gli altri teoremi. Successivamente, negli “Elementi” viene trattata anche la geometria solida in tre dimensioni che, tuttavia, in questa sezione non verrà approfondita.
Nota: Dopo Euclide sono state sviluppate particolari geometrie non basate necessariamente sui cinque postulati: queste geometrie prendono il nome di geometrie non euclidee.
Enti fondamentali
Gli enti fondamentali, o enti primitivi, sono gli elementi fondanti della geometria piana: essi sono definiti intuitivamente e permettono di definire in maniera sistematica tutti gli altri enti. I tre enti primitivi sono i seguenti:
il punto: unità adimensionale del piano
la retta: linea di lunghezza infinita nel piano, o insieme infinito di punti allineati
il piano: superficie piana di estensione infinita, o foglio infinito
Nota: Nonostante sopra si sia provato a descrivere questi concetti, quelle date non sono le loro definizioni: gli enti primitivi, in quanto tali, sono dati per noti - intuitivamente lo sono - e senza una definizione, proprio per porre un punto di inizio da cui definire tutto il resto. Senza questa assunzione è impossibile raggiungere un inizio nella catena delle definizioni: basti pensare a come, per dare l’idea di piano, si sia dovuto usare il termine superficie.
Per approfondire il piano euclideo e gli enti geometrici fondamentali si consulti la pagina "Il piano euclideo".
I cinque postulati di Euclide
I postulati della geometria euclidea sono sostanzialmente le regole di partenza a cui tutti gli enti geometrici devono sottostare. Essi sono cinque e sono i seguenti:
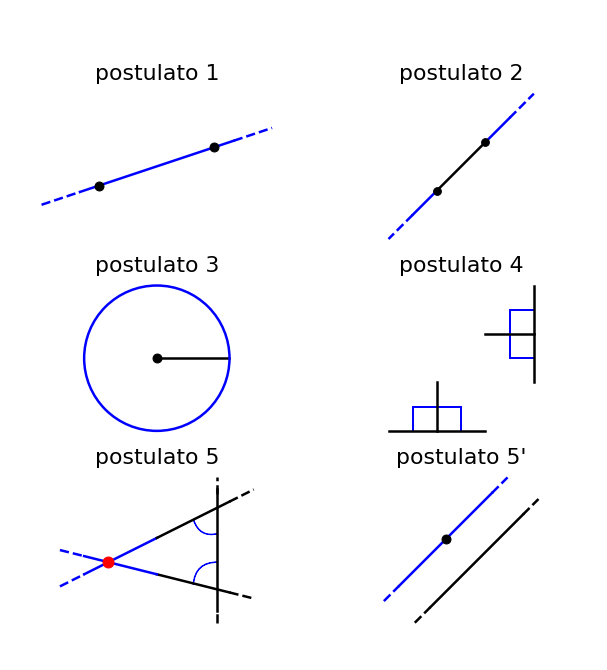
Tra due punti qualsiasi passa una e una sola retta.
Un segmento può essere prolungato indefinitamente oltre i due punti estremi.
Dato un punto e una lunghezza è possibile descrivere un cerchio.
Tutti gli angoli retti sono congruenti tra loro.
Se una retta che taglia altre due rette determina dallo stesso lato angoli interni la cui somma è minore di due angoli retti, prolungando le due rette, esse si incontreranno dalla parte dove i due angoli hanno somma minore di due retti.
Nota: Nei cinque postulati di Euclide si nota subito una differenza fra i primi quattro e il quinto, in termini di formulazione e immediatezza. Una riformulazione moderna del quinto postulato, di più facile comprensione, è la seguente:
5. Per un punto esterno a una retta data passa una e una sola retta parallela a questa.
Corollari dei postulati di Euclide
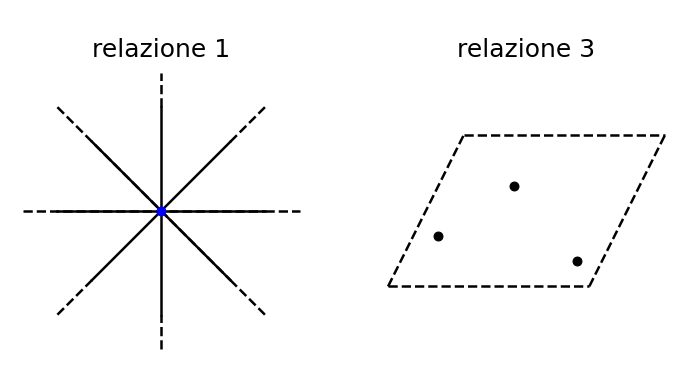
Dai cinque postulati di Euclide è possibile dedurre delle relazioni tra gli enti geometrici fondamentali: punti, rette e piani. Le principali relazioni sono le seguenti:
Per un punto passano infinite rette.
Per una retta nello spazio passano infiniti piani.
Per tre punti non allineati nello spazio passa uno e un solo piano.
Inoltre si definiscono altri enti geometrici, quali:
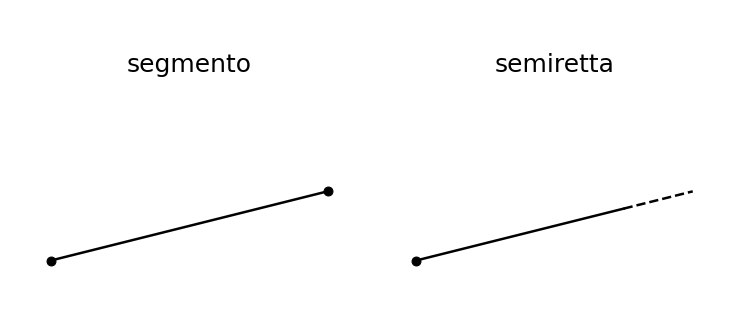
il segmento: è definito come la parte di retta delimitata da due punti distinti
la semiretta: origina da una retta che viene divisa in due parti da un punto; ciascuna parte è una semiretta, caratterizzata da un’origine ma senza un fine
Curiosità
Nel 1899, il matematico tedesco David Hilbert mette in evidenza come, nei postulati di Euclide, siano impliciti ulteriori assunti: propone quindi, nel "Grundlagen der Geometrie", un nuovo sistema assiomatico per la geometria euclidea fondato su 21 assiomi.