Cosa sono i Monomi: definizione, caratteristiche ed esempi
Nell'ambito dell'algebra, i monomi costituiscono una categoria fondamentale di espressioni matematiche. Essi rappresentano un aspetto cruciale della comprensione dell'algebra e sono alla base di molti concetti matematici più avanzati.
I monomi sono espressioni algebriche in cui compaiono solamente moltiplicazioni tra elementi numerici e elevamenti a potenza di lettere aventi come esponente numeri naturali.
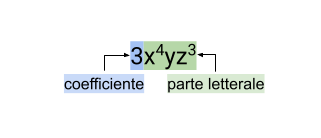
Ogni monomio è composto da due parti, la parte numerica del monomio viene definita coefficiente, mentre le lettere compongono la parte letterale del monomio.
Tipicamente, un monomio assume la forma \(ax^n\), dove:
a è il coefficiente numerico. Può essere un numero reale, intero o anche un termine costante, come 5 o −3
x rappresenta la variabile. È l'incognita o la grandezza variabile all'interno dell'espressione.
n è l'esponente della variabile. Deve essere un numero intero non negativo.
Alcuni esempi di monomi
Di seguito vengono mostrati alcuni esempi pratici di monomi:
\(2x\) è un monomio con coefficiente 2 e parte letterale x
\(-7y^2\) è un monomio con coefficiente -7 e parte letterale \(y^2\)
\(-xy^3\) in questo caso il coefficiente del monomio è -1 mentre la parte letterale è \(xy^3\)
3 è considerato un monomio in quanto può essere rappresentato come \(3x^0\), dove la variabile ha un esponente zero.
Di seguito vengono mostrati alcuni esempi di NON monomi:
\(\frac{1}{2}(2x + y)\)
\(2a + 1\)
\(\frac{x}{z}\)
\(y^{-2}\)
Caratteristiche dei monomi
I monomi presentano diverse caratteristiche distintive:
Coefficiente: Il coefficiente è il fattore numerico del monomio. Esprime la scala o l'ampiezza del monomio. Ad esempio, in \(3x^2\), il coefficiente è 3
Variabile: La variabile rappresenta l'elemento variabile del monomio. Può essere qualsiasi lettera o simbolo che indica l'incognita. In \(5y^3\), la variabile è y
Esponente: L'esponente è un numero intero non negativo che indica il grado della variabile nel monomio. Indica quante volte la variabile è moltiplicata per se stessa. Per esempio, in \(x^4\), l’esponente è 4
I monomi sono fondamentali nell'algebra e nella risoluzione di equazioni matematiche. Essi fungono da mattoni fondamentali nella costruzione di concetti più complessi come i polinomi e le equazioni.
In alcuni casi i monomi con esponenti negativi (come \(y^{-2}\)) sono ammessi sotto il nome di monomi frazionari, ma in realtà si trattano di frazioni algebriche. Inoltre nei monomi non compaiono operazioni di somma e sottrazione, perché in quei casi prendono il nome di polinomi, cioè una somma algebrica di monomi.
Nota: Un qualsiasi numero può essere definito un monomio. Consideriamo ad esempio il numero 3. Tale numero può essere riscritto nel seguente modo: \(3x^0\) (dato che \(x^0\) = 1), che si tratta proprio di un monomio essendo una moltiplicazione tra un numero e una lettera con esponente naturale. In particolare un monomio senza parte letterale viene detto monomio costante.
Nota: Il numero 0 viene definito monomio nullo
In conclusione, i monomi rappresentano una parte essenziale dell'algebra e della matematica in generale. Comprendere la loro struttura e le loro proprietà è fondamentale per affrontare concetti più avanzati. Il loro studio fornisce una solida base per esplorare argomenti più complessi come le equazioni polinomiali, le disequazioni e le applicazioni pratiche in vari campi scientifici e tecnologici.