Operazioni tra segmenti: somma, differenza, multipli

La comprensione delle operazioni tra segmenti è fondamentale per risolvere problemi geometrici complessi e per costruire figure geometriche precise.

In questa pagina esploreremo in dettaglio le operazioni di somma, differenza e multipli tra segmenti, illustrando le loro proprietà e fornendo esempi pratici per chiarire come applicare questi concetti.

Definizione di segmento

Un segmento è una parte di una retta delimitata da due punti distinti, chiamati estremi. Se A e B sono i due estremi, il segmento è indicato come AB. La lunghezza del segmento è la distanza tra i punti A e B.

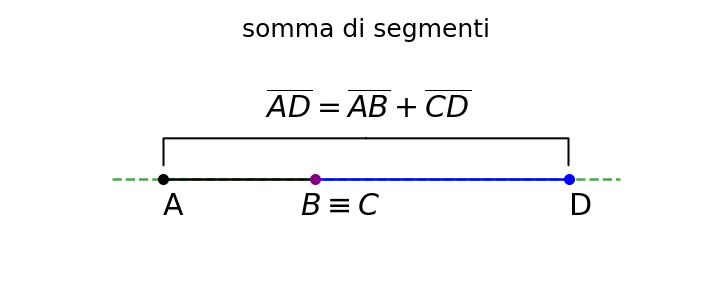
Somma di segmenti

La somma di due segmenti è un'operazione che permette di combinare due segmenti per ottenere un segmento equivalente alla somma delle loro lunghezze. Questa operazione è utile per costruire segmenti di lunghezza desiderata partendo da segmenti noti.

Proprietà della somma di segmenti:

• Commutativa: la somma di due segmenti è commutativa, cioè l'ordine in cui si sommano i segmenti non influenza il risultato. Se AB e CD sono due segmenti, allora AB + CD = CD + AB

• Associativa: la somma di segmenti è associativa, cioè la somma di più segmenti può essere raggruppata in qualsiasi modo senza cambiare il risultato. Se AB, CD e EF sono segmenti, allora (AB+CD) + EF = AB + (CD + EF)

Esempio di somma tra segmenti

Consideriamo due segmenti AB e CD con lunghezze di 3 cm e 5 cm rispettivamente. La somma dei due segmenti sarà un nuovo segmento di lunghezza 3 cm + 5 cm = 8 cm. Questo significa che possiamo combinare i segmenti AB e CD per ottenere un segmento lungo 8 cm.

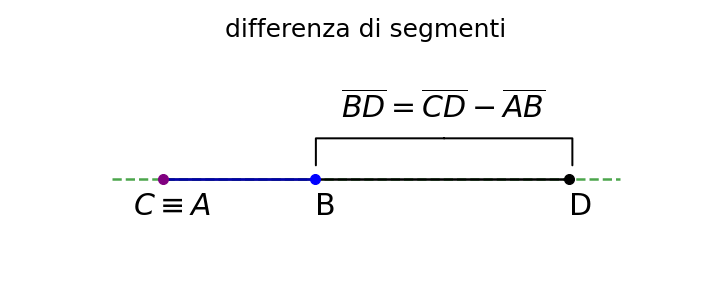
Differenza tra segmenti

La differenza tra due segmenti è un'operazione che permette di ottenere un segmento la cui lunghezza è la differenza delle lunghezze dei segmenti originali. Questa operazione è utile per determinare la lunghezza rimanente quando un segmento è parzialmente sottratto da un altro.

Proprietà della differenza tra segmenti:

• Non commutativa: la differenza tra due segmenti non è commutativa, cioè l'ordine in cui si sottraggono i segmenti influisce sul risultato. Se AB e CD sono due segmenti, generalmente AB - CD è diverso da CD - AB

• Differenza positiva: la differenza tra due segmenti è definita solo se la lunghezza del segmento da cui si sottrae è maggiore o uguale alla lunghezza del segmento che si sottrae.

Esempio di differenza tra segmenti

Consideriamo due segmenti AB e CD con lunghezze di 8 cm e 5 cm rispettivamente. La differenza dei due segmenti sarà un nuovo segmento di lunghezza 8 cm−5 cm=3 cm. Questo significa che possiamo sottrarre il segmento CD dal segmento AB per ottenere un segmento lungo 3 cm.

Multipli di segmenti

I multipli di un segmento sono segmenti che hanno lunghezza multipla rispetto al segmento originale. Questa operazione è utile per creare segmenti più lunghi partendo da segmenti di lunghezza nota.

Proprietà dei multipli di segmenti:

• Moltiplicazione per un numero intero positivo: Moltiplicare un segmento per un numero intero positivo n significa ottenere un nuovo segmento la cui lunghezza è n volte la lunghezza del segmento originale.

• Moltiplicazione per zero: oltiplicare un segmento per zero significa ottenere un segmento di lunghezza zero, che è semplicemente un punto.

Esempio di multipli di segmenti

Consideriamo un segmento AB con lunghezza di 4 cm. Se vogliamo ottenere un segmento che sia il triplo della lunghezza di AB, moltiplichiamo per 3: 3×4 cm=12 cm. Questo significa che possiamo costruire un segmento lungo 12 cm a partire dal segmento AB.

Conclusione

Le operazioni tra segmenti – somma, differenza e multipli – sono strumenti fondamentali in geometria. Comprendere come combinare, sottrarre e moltiplicare segmenti permette di costruire e analizzare figure geometriche con precisione.