Coniugato di un numero complesso

Nella pagina "Numeri complessi e campo complesso" è stato introdotto il campo complesso descrivendone gli elementi, le operazioni e le proprietà. In questa pagina ci si concentra su un particolare elemento che prende il nome di complesso coniugato.

Riassumendo, il campo complesso è un insieme di numeri, detti appunto numeri complessi, definito come:

ℂ  ≔ {(x,y) | x,y ∈ ℝ}

cioè l’insieme delle coppie ordinate (x,y) con x, y numeri reali. In particolare è definito con i ≔ (0,1) l’unità immaginaria che distingue il campo complesso dal campo reale.

In ℂ sono definite le seguenti operazioni di somma e prodotto:

(a,b) + (c,d) = (a+c,b+d)

(a,b)(c,d) = (ac-bd,bc+ad)

Sia quindi dato un generico numero complesso z = (x,y) nel piano di Gauss.

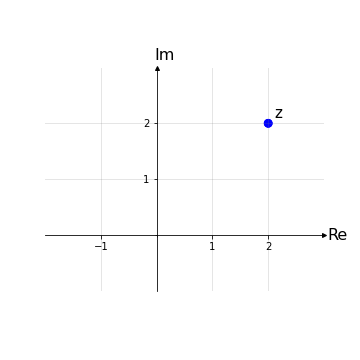
Il coniugato di z, o complesso coniugato, è definito come \(\overline{z}\) ≔ (x,-y). Nel piano di Gauss questa operazione equivale a prendere il simmetrico di z rispetto all’asse reale, Re(z).

Nota: Altre notazione per il complesso coniugato sono z* oppure conj(z).

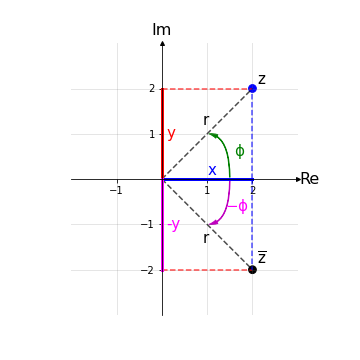
Come si vede dal grafico sopra in coordinate cartesiane si hanno:

Re(z) = Re(\(\overline{z})\)

Im(z) = - Im(\(\overline{z})\)

mentre in coordinate polari:

\(r_z = r_{\overline{z}}\)

\(\phi_z = - \phi_{\overline{z}}\)

Dato z = (x,y) = (r,Φ) avremo quindi nelle varie rappresentazioni i seguenti risultati:

• rappresentazione cartesiana:

  \(z = x + iy \quad \overline{z} = x - iy\)

• rappresentazione trigonometrica:

  \(z = r(cos\phi + isin\phi) \quad \overline{z} = r(cos\phi - isin\phi)\)

  ricordando che cos(-Φ) = cosΦ mentre sin(-Φ) = - sinΦ

• rappresentazione esponenziale: 

  \(z = r e^{i\phi} \quad \overline{z} = r e^{-i\phi}\)

Proprietà del complesso coniugato

Il complesso coniugato è caratterizzato dalle seguenti proprietà:

• \(\overline{z_1}\pm \overline{z_2} = \overline{z_1\pm z_2}\)

• \(\overline{z_1}\cdot \overline{z_2} = \overline{z_1 \cdot z_2}\)

• \(\frac{\overline{z_1}}{\overline{z_2}} = \overline{(\frac{z_1}{z_2})}\)

• \(z + \overline{z} = 2 Re(z)\)

• \(z - \overline{z} = 2 i Im(z)\)

• \(z \cdot \overline{z} = x^2+y^2 = |z|^2\) con |z| un altra notazione per indicare il modulo di z

• \(\overline{\overline{z}} = z\)

• \(\overline{z} = z \iff z \in \mathbb{R}\)

• \(|\overline{z}| = |z|\)

Le proprietà dove compare l’operazione di somma/differenza sono facilmente dimostrabili con la rappresentazione cartesiana mentre dov’è usata l’operazione di prodotto/divisione è più rapido usare la rappresentazione esponenziale.

Osservazione: ∀z ∈ ℂ-{0}, si ha:

\(\frac{1}{z} = \frac{\overline{z}}{|z|^2}\)

Prova:

\(\frac{1}{z} = \frac{1}{z} \frac{\overline{z}}{\overline{z}} =  \frac{\overline{z}}{z \cdot \overline{z}} = \frac{\overline{z}}{|z|^2}\)

dove abbiamo usato la sesta delle proprietà del complesso coniugato elencate sopra.

Per esercizio proviamo a mostrare alcune delle proprietà enunciate mentre le altre sono lasciate per esercizio per fare pratica.

Proprietà 1: Siano z₁, z₂ due numeri complessi che per semplicità di conto rappresentiamo in forma cartesiana. Segue allora che:

\(\overline{z_1} + \overline{z_2} = (x_1-iy_1)+(x_2-iy_2) = (x_1+x_2)-i(y_1+y_2) = \overline{(x_1+x_2)+i(y_1+y_2)} = \overline{z_1 + z_2}\)

Proprietà 3: Siano z₁, z₂ due numeri complessi che per semplicità di conto rappresentiamo in forma esponenziale. Segue allora che:

\(\frac{\overline{z_1}}{\overline{z_2}} = \frac{r_1 e^{-i\phi_1}}{r_2 e^{-i\phi_2}} = \frac{r_1}{r_2} e^{i(-\phi_1+\phi_2)} = \frac{r_1}{r_2} e^{-i(\phi_1-\phi_2)} = \overline{\frac{r_1}{r_2} e^{i(\phi_1-\phi_2)}} = \overline{(\frac{z_1}{z_2})}\)

Proprietà 5: Sia dato il numero complesso z = (x,y) che rappresentiamo in forma cartesiana per immediatezza del conto. Segue allora che:

\(z - \overline{z} = (x+iy)-(x-iy) = (x-x) + i(y-(-y)) = 2iy = 2 i Im(z)\)

Proprietà 6: Sia dato il numero complesso z = (r,Φ) che rappresentiamo in forma esponenziale per evitare conti inutilmente lunghi.

\(z \overline{z} = r e^{i\phi} r e^{-i\phi} = r^2 e^{i(\phi-\phi)} = r^2 = |z|^2\)