Elevamento a potenza nel piano di Gauss
Nella pagina "Numeri complessi e campo complesso" è stato introdotto il campo complesso descrivendone gli elementi, le proprietà e le operazioni su esso definite mentre nella pagina "Operazioni in campo complesso" sono state elencate molte delle operazioni coi numeri complessi anche usando diverse rappresentazioni. In questa pagina ci si concentra sull’elevamento a potenza di un numero complesso e la visualizzazione di tale operazione nel piano di Gauss.
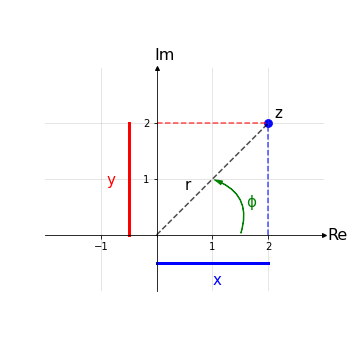
Sia dato un generico numero complesso z = (x,y) nel piano di Gauss che possiamo anche riscrivere in coordinate polari come z = (r,Φ) legate alle coordinate cartesiane dalla seguente relazione:
\(\left\{\begin{array}{@{}l@{}l} r = \sqrt{x^2+y^2}\\ \phi = arctan(\frac{y}{x})\\ \end{array}\right.\,\)
r ∈ [0,+∞) e Φ ∈ [0,2𝜋) oppure Φ ∈ (-𝜋,𝜋]
con r detto modulo e Φ detto argomento di z.
Nota: La formula per Φ vale solo se l’elemento z è situato nel primo quadrante del piano di Gauss. Qua non ci si dilunga ma, per capire meglio come funziona la trasformazione tra coordinate cartesiane e polari, si consulti la pagina "Cambio di rappresentazione tra numeri complessi".
Il passaggio alle coordinate polari (r,Φ) viene effettuato per snellire i conti, in quanto per la rappresentazione esponenziale di un numero complesso:
\(z = re^{i\phi}\)
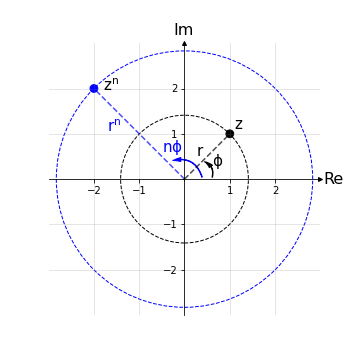
valgono le usuali regole delle potenze e in particolare la formula di De Moivre:
\(z^n = r^n e^{in\phi} = r^n(cos(n\phi) + i sin(n\phi))\) n ∈ ℕ
In sostanza dato z = (r,Φ), con l’elevamento a potenza n-esima, si ha un elevamento a potenza del modulo ed una dilatazione dell’argomento:
(r,Φ) → (rn,nΦ)
Seguono alcuni esempi con rappresentazione grafica nel piano di Gauss:
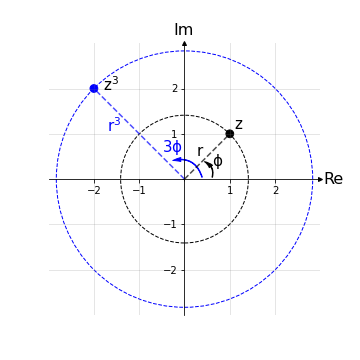
Esempio 1: Calcolare il cubo di z = 1 + i e si assuma come intervallo dell’argomento Φ ∈ [0,2𝜋).
Il primo passo è quello di passare alle coordinate polari per poi applicare la formula di De Moivre:
\(\left\{\begin{array}{@{}l@{}l} r = \sqrt{1^2+1^2} = \sqrt{2}\\ \phi = arctan(\frac{1}{1}) = \frac{\pi}{4}\\ \end{array}\right.\,\)
quindi \( z = \sqrt{2} (cos\frac{\pi}{4} + i sin\frac{\pi}{4}) \).
Applichiamo ora la formula di De Moivre per il cubo (n=3):
\begin{equation*}\begin{aligned} z^3 & = (\sqrt{2})^3 \left(cos\frac{3\pi}{4} + i sin\frac{3\pi}{4}\right)\\ & = (\sqrt{2^3}) \left(-cos\frac{\pi}{4} + i sin\frac{\pi}{4}\right)\\ & = 2\sqrt{2} \left(-\frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2}\right)\\ & = 2 (-1+i) = -2 + 2 i \end{aligned}\end{equation*}
ricordando qualche angolo notevole per seno e coseno.
In coordinate polari
\(\left\{\begin{array}{@{}l@{}l} r^3 = 2\sqrt{2}\\ 3\phi = \frac{3\pi}{4}\\ \end{array}\right.\,\)
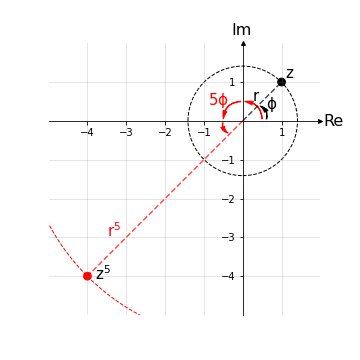
Esempio 2: Calcolare potenza quinta di z = 1 + i e si assuma come intervallo dell’argomento Φ ∈ (-𝜋,𝜋].
Dall’esercizio 1 sappiamo che \( z = \sqrt{2} (cos\frac{\pi}{4} + i sin\frac{\pi}{4}) \).
Applichiamo ora la formula di De Moivre per la potenza quinta (n=5):
\begin{equation*}\begin{aligned} z^5 & = (\sqrt{2})^5 \left(cos\frac{5\pi}{4} + i sin\frac{5\pi}{4}\right)\\ & = (\sqrt{2^5}) \left(-cos\frac{\pi}{4} - i sin\frac{\pi}{4}\right)\\ & = 4\sqrt{2} \left(-\frac{\sqrt{2}}{2} - i \frac{\sqrt{2}}{2}\right)\\ & = 4 (-1-i) = -4 + 4 i \end{aligned}\end{equation*}
In coordinate polari:
\(\left\{\begin{array}{@{}l@{}l} r^5 = 4\sqrt{2}\\ 5\phi = -\frac{3\pi}{4}\\ \end{array}\right.\,\)
e non \(5\phi = \frac{5\pi}{4}\) perché l’argomento si è chiesto essere nell’intervallo (-𝜋,𝜋].
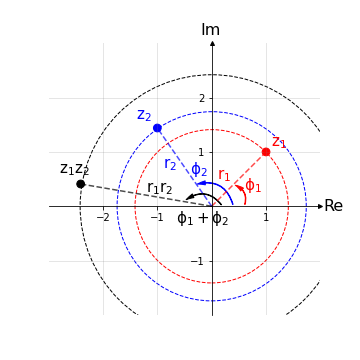
Generalizzazione al prodotto tra numeri complessi
Volendo generalizzare quanto visto al prodotto tra numeri complessi, prendiamo i seguenti elementi in coordinate polari, sempre per semplicità di calcolo:
\( z_1 = r_1 (cos\phi_1 + i sin\phi_1) \)
\( z_2 = r_2 (cos\phi_2 + i sin\phi_2) \)
Eseguendo la moltiplicazione in forma esponenziale e ricordando le proprietà delle potenze si ottiene:
\begin{equation*} \begin{aligned} z_1 z_2 & = r_1 r_2 e^{i(\phi_1+\phi_2)}\\ & = r_1 r_2 (cos(\phi_1+\phi_2) + i sin(\phi_1+\phi_2)) \end{aligned} \end{equation*}
che, nel caso z1 = z2, riconduce all’operazione z2. Nel piano di Gauss quel che succede può essere visualizzato come segue: