Coordinate cartesiane e polari per i numeri complessi

Nelle pagine "Piano di Gauss" e "Rappresentazione dei numeri complessi", sono state introdotte le varie rappresentazioni e, soprattutto, le coordinate polari. Questa pagina amplia quanto detto in "Modulo e argomento di un numero complesso" sulle relazioni che intercorrono fra coordinate cartesiane e polari e proponendo ulteriori esempi.

Ricordando che l’insieme dei numeri complessi è in corrispondenza biunivoca con il prodotto cartesiano ℝ x ℝ, anche denotato come ℝ², possiamo associare univocamente ogni numero complesso ad una coppia di coordinate del tipo (x,y): per molti aspetti ricorda il classico piano cartesiano che viene sempre usato per rappresentare funzioni reali in una variabile. Tuttavia è presente una differenza sostanziale: nel piano cartesiano gli assi x e y sono entrambi assi reali, invece, in quello che chiameremo piano di Gauss, solo l’asse orizzontale è l’asse reale (Re), mentre l’asse verticale è detto asse immaginario (Im).

Per rappresentare i numeri complessi usiamo quindi il piano di Gauss:

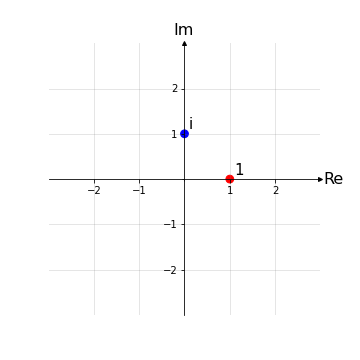
Come nel piano cartesiano è possibile rappresentare univocamente qualsiasi punto usando le coordinate cartesiane o le coordinate polari, anche nel piano di Gauss è possibile fare la stessa cosa.

Nonostante vi siano tre possibili rappresentazioni per un numero complesso, le coordinate utilizzate sono soltanto di due tipi:

• cartesiane: possono essere indicate con la stessa notazione con cui si indica un numero complesso, ovvero (x,y)

• polari: sono date dalla coppia (r,Φ)

Trasformazione di coordinate

Date le due coppie di coordinate cartesiane (x,y) e polari (r,Φ), le relazioni che intercorrono tra esse sono le seguenti:

passando da (r,Φ) → (x,y)

\(\left\{\begin{array}{@{}l@{}l} x = r cos\phi\\  y = r sin\phi \end{array}\right.\, \)

passando da (x,y) → (r,Φ) con intervallo Φ ∈ [0,2𝜋)

\(r := \sqrt{x^2+y^2}\)

\(\phi := \begin{cases} arctan(\frac{y}{x}) & \text{se $x>0$, $y\geq 0$ (I q.)} \\  arctan(\frac{y}{x})+2\pi & \text{se $x>0$, $y< 0$, (IV q.)}\\ arctan(\frac{y}{x})+\pi & \text{se $x<0$, $y< 0$, (II e III q.)}\\ \frac{\pi}{2} & \text{se $x=0$, $y>0$}\\  \frac{3\pi}{2} & \text{se $x=0$, $y<0$}\\  \text{non definito} & \text{se $x=0$, $y=0$} \end{cases}\)

passando da (x,y) → (r,Φ) con intervallo Φ ∈ (-𝜋,𝜋]

\(r := \sqrt{x^2+y^2}\)

\(\phi := \begin{cases} arctan(\frac{y}{x}) & \text{se $x>0$, $y$ qualsiasi (I e IV q.)} \\  arctan(\frac{y}{x})+\pi & \text{se $x<0$, $y\geq0$, (II q.)}\\  arctan(\frac{y}{x})-\pi & \text{se $x<0$, $y<0$, (III q.)}\\  \frac{\pi}{2} & \text{se $x=0$, $y>0$}\\  \frac{3\pi}{2} & \text{se $x=0$, $y<0$}\\ \text{non definito} & \text{se $x=0$, $y=0$} \end{cases}\)

Con dominio per (x,y)

\(\begin{cases}  x \in (-\infty,+\infty) \\  y \in (-\infty,+\infty) \end{cases}\)

e dominio per (r,Φ)

\(\begin{cases} r \in [0,+\infty) \\  \phi \in [0,2\pi) \vee (-\pi,+\pi] \text{ arbitrariamente} \end{cases}\)

Nota: La scelta dell’intervallo per Φ è arbitraria, tuttavia una volta fissato l’intervallo bisogna mantenere la coerenza della scelta.

Esempio 1: Sia dato il numero z = 5 + i, si riscriva z in coordinate polari (r,Φ) trovandone modulo |z| e argomento Arg(z).

Per il modulo applichiamo banalmente la definizione, individuando la parte reale Re(z) = 5 e la parte immaginaria Im(z) = 1. Per l’argomento invece poniamo innanzitutto come intervallo [0,2𝜋) e notiamo che Re(z), Im(z) > 0: z si trova nel primo quadrante e applichiamo la formula corrispondente.

\(\begin{cases} r = \sqrt{Re(z)^2+Im(z)^2} = \sqrt{26} \\  \phi = arctan\left(\frac{Im(z)}{Re(z)}\right) = arctan\left(\frac{1}{5}\right) \simeq 11.3^{\circ}  \end{cases}\)

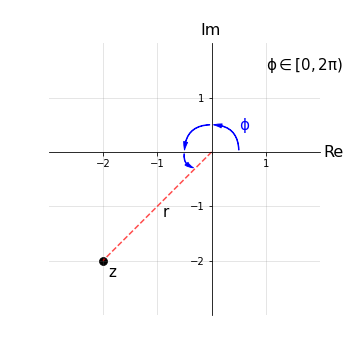
Esempio 2: Sia dato il numero z = -2 - 2i, si riscriva z in coordinate polari (r,Φ) trovandone modulo |z| e argomento Arg(z).

Si procede come nell’esercizio 1: Re(z) = -2, Im(z) = -2. Scegliamo l’intervallo [0,2𝜋) e notiamo che Re(z), Im(z) < 0: z si trova nel terzo quadrante.

\(\begin{cases}  r = \sqrt{Re(z)^2+Im(z)^2} = \sqrt{8} \\  \phi = arctan\left(\frac{Im(z)}{Re(z)}\right)+\pi = arctan(1)+\pi = \frac{5\pi}{4}  \end{cases}\)

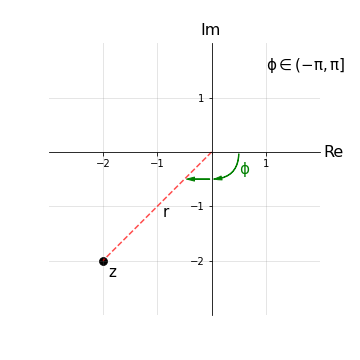
Esempio 3: Sia dato il numero z = -2 - 2i, si riscriva z in coordinate polari (r,Φ) trovandone modulo |z| e argomento Arg(z). Si assuma l’intervallo (-𝜋,𝜋].

L’unica differenza rispetto all’esempio 2 è l’intervallo di Φ, ovvero bisogna usare un’altra definizione nella trasformazione (x,y) → Φ.

\(\begin{cases} r = \sqrt{Re(z)^2+Im(z)^2} = \sqrt{8} \\  \phi = arctan\left(\frac{Im(z)}{Re(z)}\right)-\pi = arctan(1)-\pi = \frac{3\pi}{4}  \end{cases}\)

Limiti dell’arcotangente

Il motivo per cui, nel passaggio (x,y) → (r,Φ), per Φ è necessario controllare il quadrante in cui (x,y) si trova e lo stesso Φ ha un’arbitrarietà sull’intervallo è dovuto alla definizione di arcotangente: se la funzione f(z) ≔ tan(z):

f: ℝ\{2k𝜋, k ∈ ℤ} → ℝ

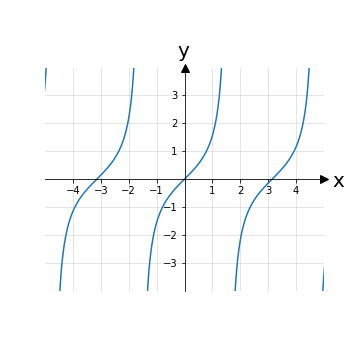
la funzione inversa f^-1 è ottenibile solo tramite una restrizione del dominio per soddisfare la condizione di iniettività:

\(\left.f\right|_{\left(-\frac{\pi}{2},\frac{\pi}{2}\right)}: \left(-\frac{\pi}{2},\frac{\pi}{2}\right) \rightarrow \mathbb{R} \)

\(f^{-1}: \mathbb{R} \rightarrow \left(-\frac{\pi}{2},\frac{\pi}{2}\right)\)

Se ne deduce che non importa quali siano Re(z) ≔ x, Im(z) ≔ y, applicando solamente la formula :

\(\phi = arctan(\frac{y}{x})\)

non possiamo rappresentare tutti i punti nel piano di Gauss ma solo quelli per Re(z) > 0. Da questo fatto si possono capire a pieno le definizioni per Φ enunciate al paragrafo sopra, ricordando la periodicità di periodo 𝜋 della funzione tangente:

• i valori che essa assume nel terzo quadrante sono gli stessi che assume nel primo

• i valori che essa assume nel secondo quadrante sono gli stessi del quarto