Funzione invertibile

Sia data la generica funzione f: X → Y, x ⟼ y ∈ f(X) ⊆ Y, si ha che ad ogni y è associato almeno un elemento x ∈ X | f(x) = y - in accordo con la definizione di funzione - e l’insieme di queste x è detto controimmagine di y. In particolare ogni x ∈ X apparterrà alla controimmagine di almeno un y. Per ulteriori chiarimenti si consulti la pagina "Funzione".

Quindi una relazione che associa gli elementi y ∈ f(X) alle rispettive controimmagini x ∈ X in generale non costituisce una funzione: data h: f(X) ⟼ X, y ⟼ x avremo che a un solo elemento y possono corrispondere più elementi x e ciò implica che h non sia una funzione.

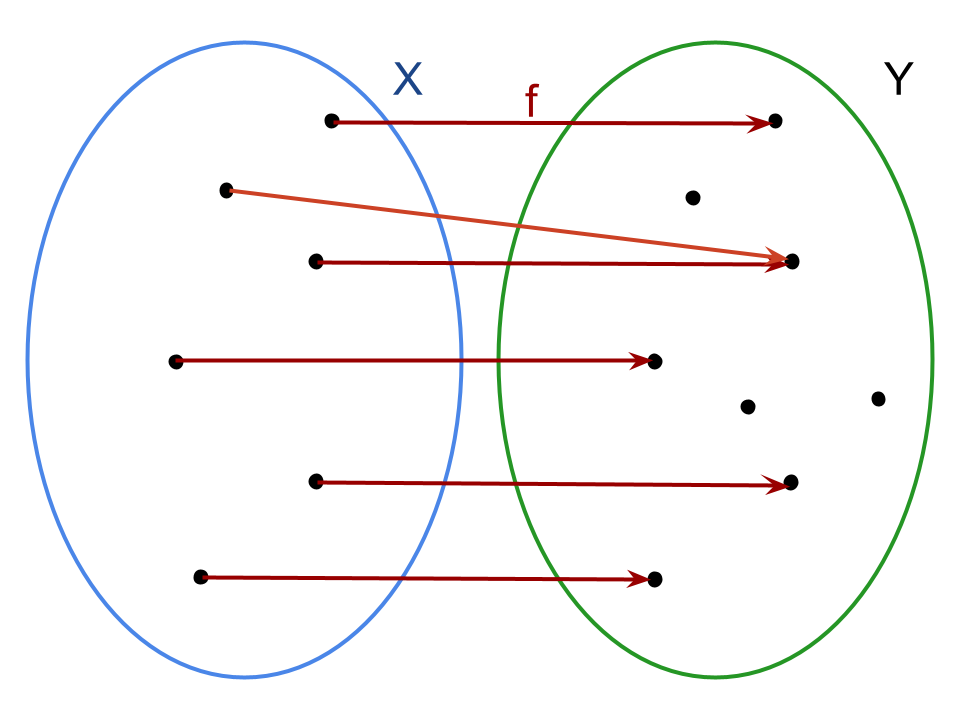
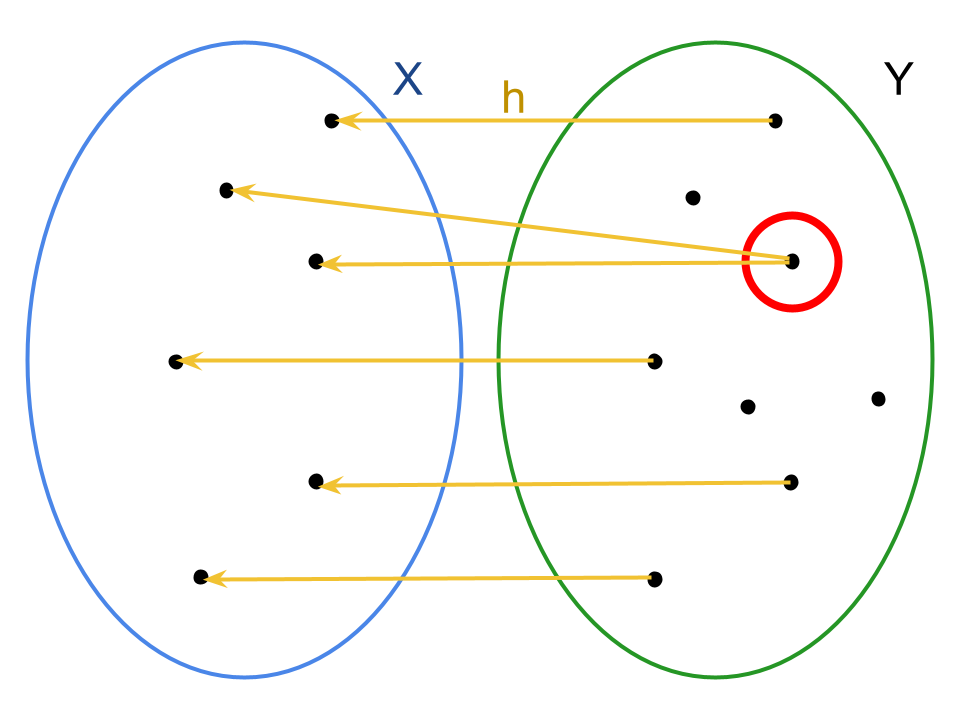
Come si può notare la funzione h non è ben definita: a un elemento del suo dominio, f(X) ⊆ Y, associa due elementi del codominio, X, e di conseguenza non è etichettabile come funzione.

Nota: Con la notazione y si fa riferimento alle sole y ∈ f(X), cioè alle sole y immagini degli elementi x ∈ X attraverso la funzione f. Per gli altri elementi del codominio, di cui f(X) è sottoinsieme, non vale quanto detto sopra; per convenzione siano denotati con y*. 

L’unica condizione che garantisce alla relazione h di essere una funzione prevede che f debba essere iniettiva: l’iniettività garantisce che la controimmagine di ogni y ∈ f(X) sia composta da un unico elemento x ∈ X e, di conseguenza, si avrà una corrispondenza biunivoca tra gli elementi y ed x.

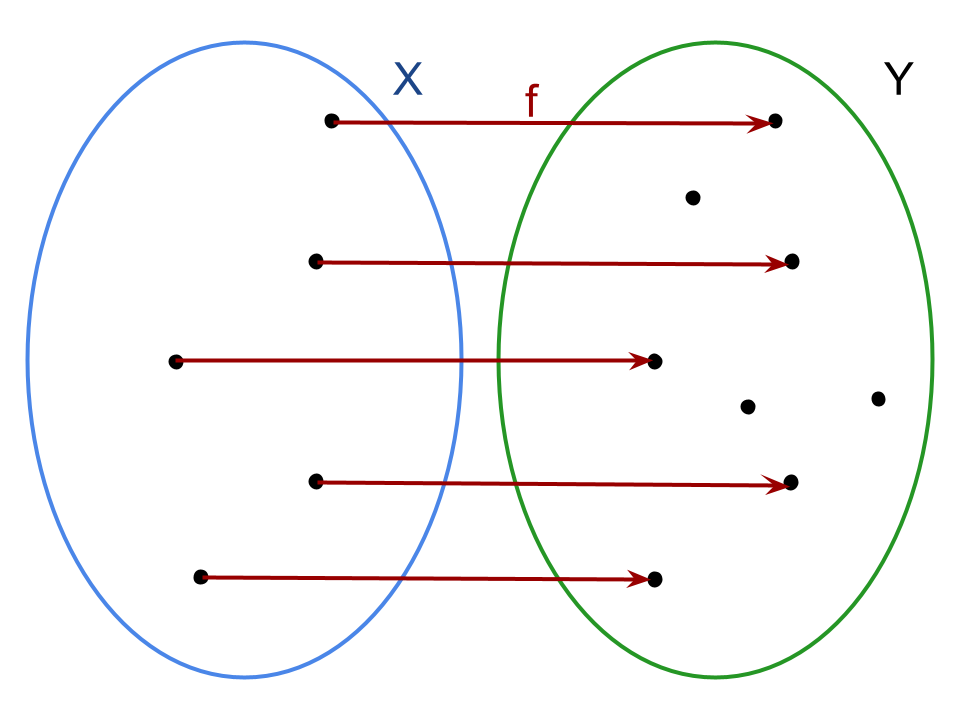
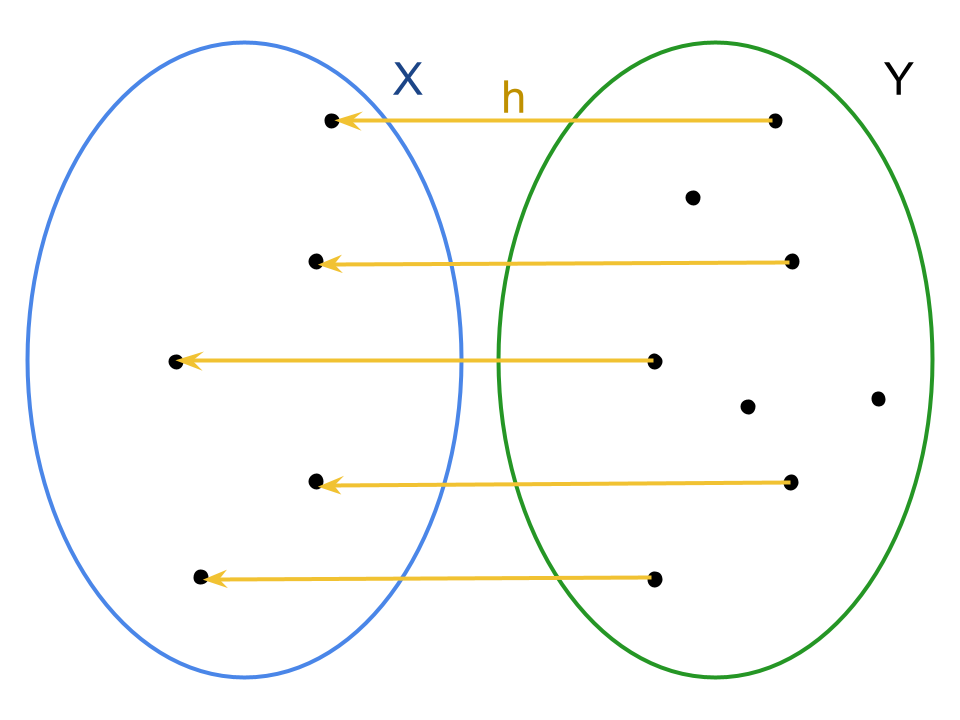
Definizione: Una funzione f: X → Y si dice invertibile se e solo se esiste una funzione che associa a ciascun elemento dell’immagine di f la sua controimmagine. Tale funzione prende il nome di funzione inversa di f e viene solitamente indicata con la notazione f^-1.

Teorema: Sia f: X → Y una funzione iniettiva, allora risulta definita una funzione h: f(X) → X, y ⟼ x dove ∀y ∈ f(x), ∃! x | h(y) = x oppure tale che f(x) = y. La funzione h è proprio la funzione inversa di f, h ≔ f^-1. In particolare, tale funzione si può dimostrare essere unica.

In altre parole succede che:

f: X → Y, x ⟼ f(x), dove y = f(x)

f^-1: f(X) → X, y ⟼ f^-1(y), dove x =  f^-1(y)

L’azione della funzione inversa può anche essere scritta come f(x) ⟼  f^-1[f(x)], dove x = f^-1[f(x)].

Osservazione: Il caso trattato finora è quello più generale possibile e infatti la funzione inversa descritta sopra necessita di avere come dominio l’insieme immagine e non il codominio della funzione. Tuttavia si ricordi che è sempre possibile ridefinire la funzione f sostituendo il codominio con lo stesso insieme immagine, grazie alla condizione di uguaglianza rilassata tra funzioni spiegata in "Uguaglianza tra funzioni".

Così facendo, avremo che oltre ad essere iniettiva per ipotesi del teorema, la funzione f: X → f(X) è anche suriettiva.

Condizione per l’invertibilità

Come accennato nel Teorema sopra, la condizione necessaria e sufficiente affinché una funzione sia invertibile è che essa sia iniettiva. A questo punto è sempre applicabile una restrizione del codominio per fare in modo che la funzione f e la sua inversa f^-1 operino tra gli stessi insiemi. Ciò non è essenziale purchè si ricordi che f^-1: f(X) → X e non Y → X .

Tuttavia, la regola comune vuole che una funzione f: X → Y sia invertibile se e solo se è biettiva, cioè sia suriettiva che iniettiva. In questo modo quello che succede è, in notazione:

f: X → f(X)=Y, x ⟼ f(x)

f^-1: Y=f(X) → X, y ⟼ f^-1(y)

senza più dover prestare particolari attenzioni all’insieme di partenza della funzione inversa, che si ritrova a coincidere con quello di arrivo della funzione di partenza: il dominio di f^-1 è il codominio/immagine di f e il codominio/immagine di f^-1 è il dominio di f.

Nota: Sulla base di quanto detto si ricordi che basta verificare solo l’iniettività della funzione f mentre la suriettività può sempre essere ottenuta con una restrizione del codominio.

Nota: Si presti attenzione al fatto che f^-1(x) ≠ [f(x)]^-1 = 1 / f(x) cioè la notazione f^-1 non indica un elevamento a potenza della funzione f.

Esempi con funzioni reali di variabili reali

Nella spiegazione sopra ci si è voluti mantenere nel caso più generale possibile, tuttavia il concetto di funzione invertibile si applica soprattutto a funzioni reali di variabile reale. Qui elenchiamo solo alcuni esempi: per il calcolo esplicito della funzione inversa invece rimandiamo alla pagina “Funzione inversa”.

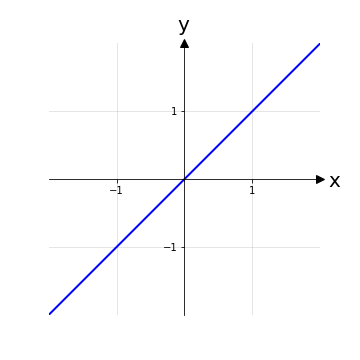
Esempio 1: Sia data la funzione f: ℝ → ℝ con legge y = x, cioè la funzione identità. Tale funzione si può verificare essere iniettiva su tutto il dominio ℝ, cioè ∀x₁,x₂ ∈ ℝ, x₁ ≠ x₂ ⇔ f(x₁) ≠ f(x₂); graficamente ciò si traduce nel fatto che nessuna retta parallela all’asse x interseca il grafico della funzione in più di un punto. La suriettività è anch’essa verificata quindi non è necessario operare una restrizione sul codominio: la funzione identità è biettiva e quindi, per il teorema sopra, anche invertibile. In particolare la funzione inversa di f è la stessa funzione identità.

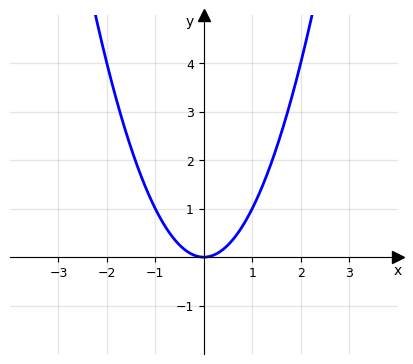
Esempio 2: Sia data la funzione f: ℝ → ℝ con legge y = x², la classica parabola. Tale funzione si verifica non essere iniettiva sul dominio ℝ: in particolare ∀x₁ ∈ ℝ⁺, ∃x₂ ∈ ℝ^- tale che f(x₁) = f(x₂) per il fatto che l’elevamento a una potenza pari fa "perdere" traccia del segno della base. La funzione f quindi, per come è stata definita, non è iniettiva e di conseguenza, essendo questa condizione necessaria per l'invertibilità, non invertibile.

Tuttavia è possibile, operando una restrizione sul dominio, prende un ramo di questa parabola che sia iniettivo sul suo dominio e, visto che ci siamo, possiamo restringere il codominio da ℝ a ℝ₀⁺ in modo da avere anche la suriettività. La nuova funzione f* sarà quindi definita con la stessa legge y = x² ma tra gli insiemi f*: ℝ⁺₀ → ℝ⁺₀ che si può verificare essere biettiva e quindi invertibile. La funzione inversa sarà data dalla legge inversa \(y=\sqrt{x}\). 

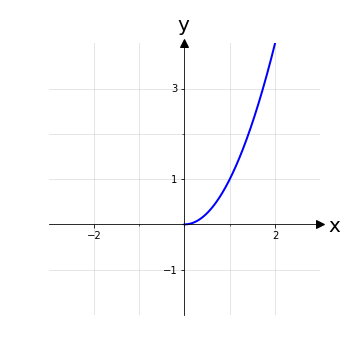
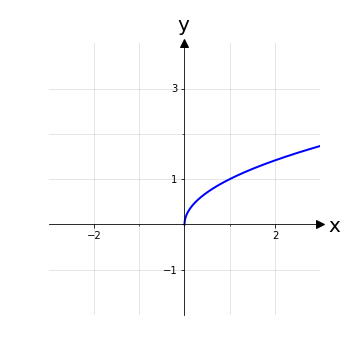
Si noti che sarebbe stato possibile considerare anche la funzione f**: ℝ^-₀ → ℝ⁺₀, x ⟼ x² e anche questa sarebbe stata invertibile con legge della funzione inversa y=-x.

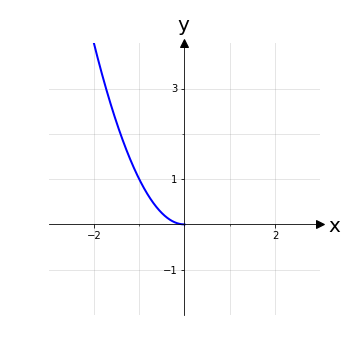
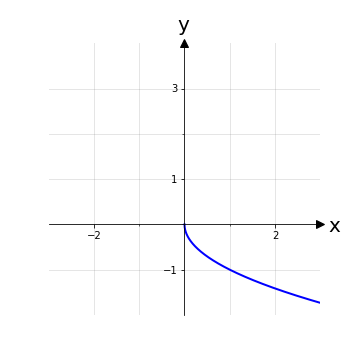
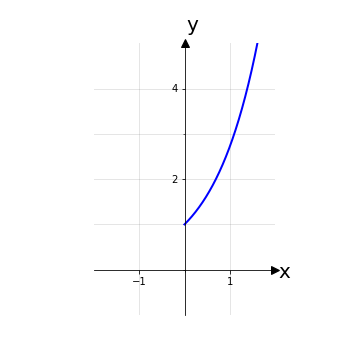
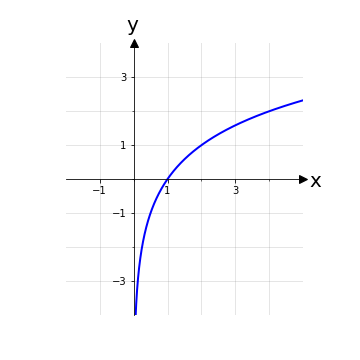
Esempio 3: Un esempio classico di funzione invertibile è la funzione esponenziale f: ℝ → ℝ⁺, x ⟼ e^x che è invertibile, con funzione inversa la funzione logaritmica f^-1: ℝ⁺ → ℝ, x ⟼ ln(x). La funzione esponenziale è iniettiva e l’unica attenzione è da rivolgere al codominio in modo da renderla suriettiva per poter usare lo stesso insieme come dominio della funzione logaritmica.

Nota: Solitamente si utilizza la notazione ℝ⁺ per indicare l’insieme ℝ⁺ ≔ {x ∈ ℝ | x > 0} mentre con ℝ⁺₀ ≔  {x ∈ ℝ | x ≥ 0} si indica lo stesso insieme con l’aggiunta dello zero.

Dettagli sulla funzione invertibile e la sua inversa

Sia data una funzione invertibile f e la sua funzione inversa f^-1, allora la composizione tra le due funzioni è la funzione identità id_S, dove S è l’insieme di partenza e arrivo. Assumiamo f(X) = Y per semplicità, allora abbiamo:

f: X → Y, x ⟼ f(x)

f^-1: Y → X, y ⟼ f^-1(y)

f ° f^-1 = f(f^-1(y)) = id_y = y

f^-1 ° f = f^-1(f(x)) = id_x = x

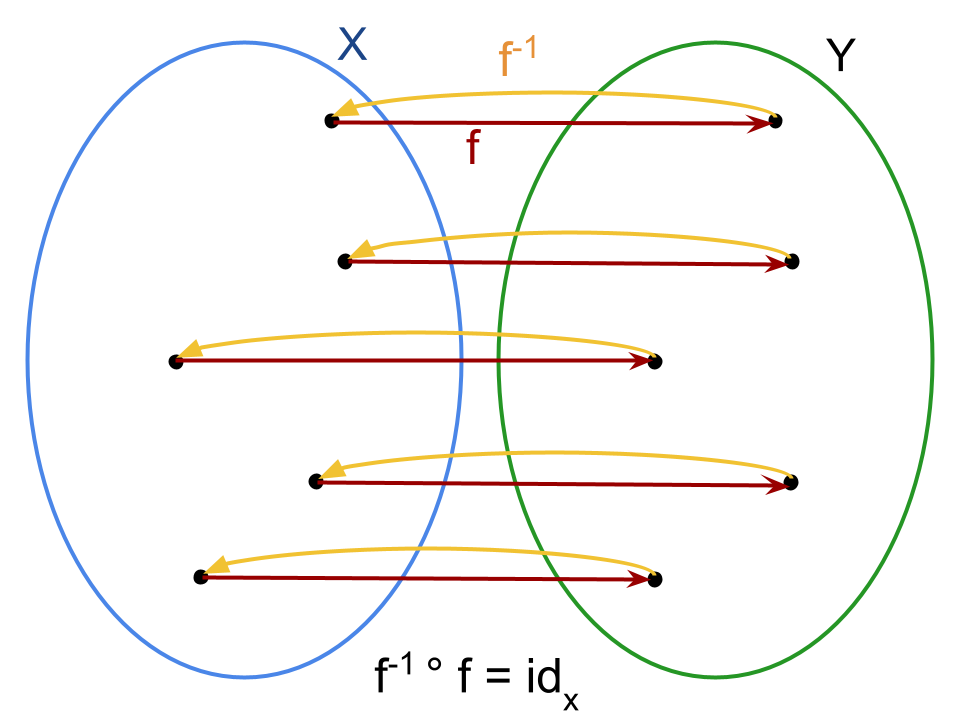
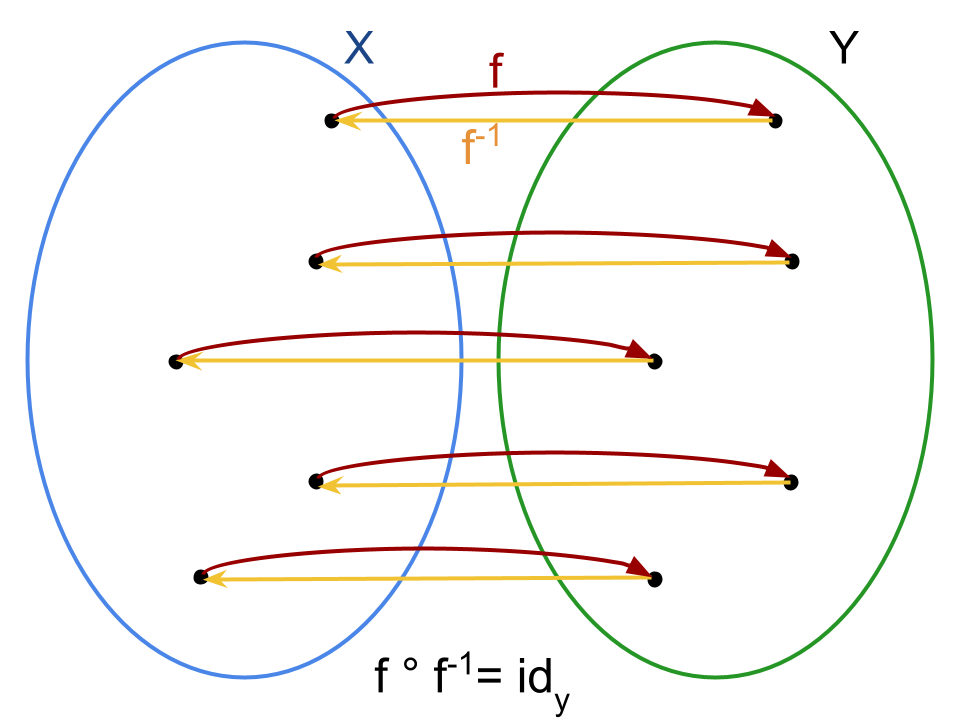
L’operazione da svolgere prima nella composizione di funzioni è quella a destra. Per avere un’idea su che insiemi stiamo operando basta applicare la definizioni delle singole funzioni:

f^-1: Y → X, f: X → Y  e quindi  f ° f^-1: Y → Y

f: X → Y, f^-1: Y → X  e quindi  f^-1 ° f: X → X

come suggeriscono le rappresentazioni con i diagrammi di Venn sopra.

Una funzione invertibile presenta inoltre altre utili proprietà rispetto alla composizione tra funzioni e rispetto all’operazione di derivazione.

Nota: Le variabili in generale sono mute, ovvero sostituire x a y non avrebbe cambiato il senso delle operazioni; tuttavia per chiarezza si è cercato di mantenere una certa coerenza.
Per vedere alcuni metodi grafici e algebrici per rappresentare la funzione inversa si rimanda alla pagina “Grafico di una funzione inversa e legge analitica”.