Definizione di funzione

Dati due insiemi X, Y, una funzione f da X in Y è una qualsiasi relazione che manda elementi x ∈ X in elementi y ∈ Y, associando ad ogni elemento di X un e un solo elemento di Y. In linguaggio matematico quanto detto sopra si può tradurre come segue: f: X → Y \(\; \forall\: x \in X, \exists!\: y \in Y \; |\; y=\!f(x) \) dove con f(x) ci si riferisce all’applicazione della funzione f sull’elemento x.

NOTA: Ci sono diversi modi, tra loro equivalenti, per esprimere la definizione di funzione. Per semplicità qui è stato riportato solo il più comune; tuttavia, per chi voglia inquadrare il concetto da altri punti di vista, è stata dedicata una pagina apposita dove si analizza più nello specifico il legame tra funzione, relazione e prodotto cartesiano.

Per avere una rappresentazione grafica di quello che succede quando si definisce una funzione tra due insiemi si analizzi il seguente grafico:

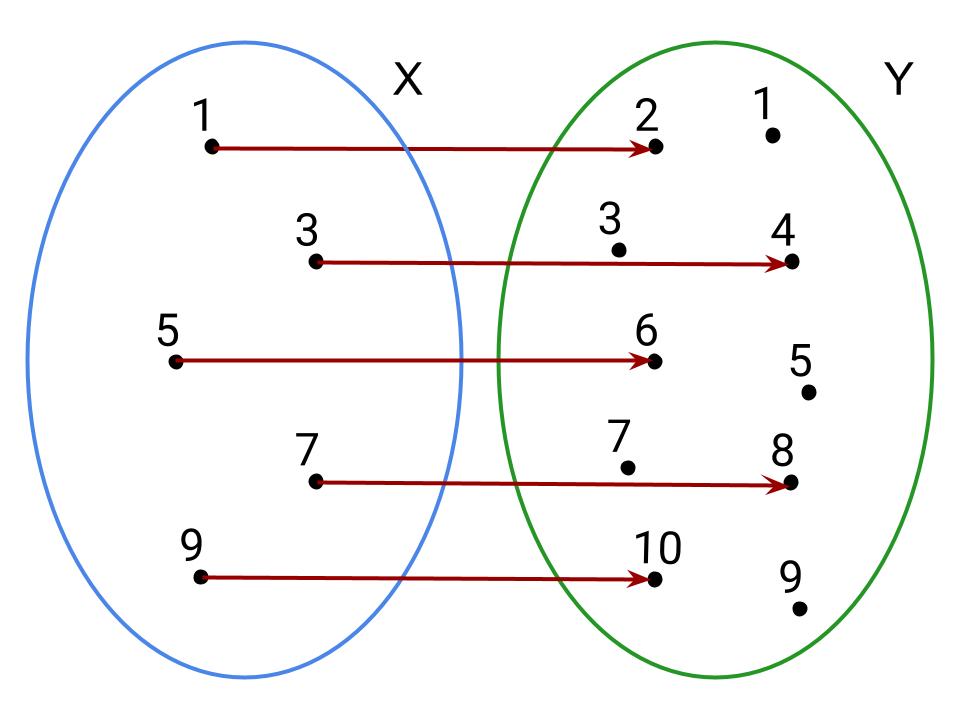
Nello specifico la funzione disegnata mette in relazione i numeri dispari minori di 10, contenuti nell’insieme X, con i rispettivi numeri pari successivi, contenuti nell’insieme Y. Importante è notare come la funzione in esame metta in relazione tutti gli elementi di X con alcuni elementi di Y e lo fa assegnando un solo y ∈ Y per ogni x ∈ X.

NOTAZIONE: Una delle possibili notazioni per le funzioni è la seguente: \( f: X → Y, x ⟼ f(x)\) con \( y \in Y \: \land \: y=f(x) \) dove f è una funzione da X, insieme di partenza, a Y, insieme di arrivo. Il simbolo → mette in relazione i due insiemi mentre il simbolo ⟼ precisa la relazione tra i singoli elementi. Generalmente le funzioni vengono indicate con le lettere minuscole.

Esempio 1: Sia X l’insieme delle persone e Y l’insieme dei genitori biologici. L’associazione persona ⟼ genitore non è una funzione in quanto ogni persona ha 2 genitori biologici e quindi l’associazione non risulta univoca. In termini matematici ad un elemento x non è associato un unico elemento y.

Esempio 2: Sia X l’insieme ℕ. La relazione X → X | x ⟼ x, ovvero la relazione che associa ad ogni elemento di X sè stesso è una funzione da X in X, detta funzione identità I_x.

Esempio 3: Sia X l’insieme ℝ. La relazione X → X | x ⟼ x + 2 è univoca e quindi è una funzione: dati un numero x ne esiste solo uno la cui differenza rispetto a y sia pari a 2.

Esempio 4: Sia X l’insieme ℝ. La relazione X → X | x ⟼ 1 è univoca e quindi è una funzione: non ci deve preoccupare il fatto che ad ogni elemento dell’insieme di partenza sia associato lo stesso elemento dell’insieme di arrivo. L’importante è, come ripetuto più volte, che ad ogni elemento dell’insieme di partenza sia associato un e un solo elemento dell’insieme di arrivo e nulla vieta che possa ripetersi.

Sia una funzione f : X → Y. L’insieme X di partenza verrà denominato dominio di f - dom(f) - mentre l’insieme Y di arrivo verrà detto codominio di f - cod(f).

Inoltre si definisce insieme immagine, im(f) o f(X), la classe di tutti i punti f(x): dato f: X → Y diremo immagine di X tramite f l’insieme f(X) ≔ { y ∈ Y | ∃ x ∈ X | y = f(x) } che, tradotto in linguaggio comune, descrive f(X) come l’insieme di tutti gli elementi y per i quali esiste un elemento x rispetto al quale sono immagine - attraverso la funzione f.

In particolare il singolo elemento y, con y=f(x), è detto immagine dell’elemento x, mentre x viene detto controimmagine di y. L’insieme delle controimmagini sarà banalmente il dominio, per definizione, mentre l’insieme di tutte le immagini attraverso la funzione f sarà appunto l’insieme immagine f(X).

Esempio 5: Nella funzione rappresentata nel grafico sopra, l’insieme immagine corrisponde all’insieme {2, 4, 6, 8, 10}.

NOTA: La definizione di codominio varia da testo a testo ma vale sempre f(X) ⊆ Y, ovvero che l’insieme immagine è sottoinsieme del codominio. Per alcuni testi questi possono non coincidere ma è una questione puramente linguistica.

Esempio 6: Sia f: ℝ → ℝ | x → x². Tale f è una funzione che ha come dominio e codominio lo stesso insieme dei numeri reali ℝ; tuttavia studiando l’insieme immagine f(X) si scopre che esso è costituito da elementi maggiori o uguali a 0 e mai negativi. Questo implica cod(f) ≠ f(X) poiché il codominio ammette anche valori negativi in quanto insieme ℝ.

Funzioni numeriche

Le funzioni che possiedono come dominio (insieme di partenza) e codominio (insieme di arrivo) degli insiemi numerici, sono dette funzioni numeriche. In particolare svolgono un ruolo importante le funzioni che hanno come dominio e codominio sottoinsiemi dell’insieme ℝ dei numeri reali, ovvero del tipo f: ℝ → ℝ. Tali funzioni sono dette funzioni reali di variabile reale. Esse saranno descrivibili mediante una delle seguenti notazioni:

• espressione analitica della funzione, per esempio f(x) = x + 2
• equazione della funzione, ovvero y=f(x) dove f(x) è l’espressione analitica: per esempio y = x+2

Variabile dipendente e variabile indipendente

Consideriamo l’equazione generale di una funzione, y=f(x).
Il valore che assume y dipende da quello attribuito a x: di conseguenza y prende il nome di variabile dipendente, mentre x di variabile indipendente. Di fatto alla variabile x può essere assegnato un valore arbitrario del dominio della funzione, mentre per la variabile y questo non è possibile, poiché il valore di y è legato alla x scelta.