Definizioni alternative di funzione

In aggiunta a quanto riportato nella pagina Funzioni, sono qui riportate delle definizioni alternative del concetto di funzione per analizzare nello specifico il suo legame con relazioni e prodotto cartesiano.

Definizione 1

Dati due insiemi X, Y, una funzione f da X in Y è una qualsiasi relazione che manda elementi x ∈ X in elementi y ∈ Y, associando ad ogni elemento di X un e un solo elemento di Y. In linguaggio matematico quanto detto sopra si può tradurre come segue: \(f: X → Y, \forall \; x \in X,\; \exists! \; y \in Y \; | \; y=f(x) \) dove con f(x) ci si riferisce all’applicazione della funzione f sull’elemento x.

Questa è la definizione più comune, riportata anche nella pagina principale. I punti cardine della definizione sono i seguenti:

• Una funzione è una relazione: in quanto tale darà origine a coppie ordinate e per questo viene effettuata la distinzione tra insieme di partenza e insieme di arrivo.
• A tutti gli elementi di X, insieme di partenza, deve essere associato un unico qualsiasi elemento di Y, insieme di arrivo. Se ciò non è verificato si può ricondurre a due cause non esclusive tra loro:
  1. Non tutte le x formano una coppia ordinata con un rispettivo y: questo problema può essere risolto con una restrizione del dominio, ovvero considerando un sottoinsieme A ⊆ X che contenga solo gli elementi x che soddisfano la relazione y=f(x).
  2. Qualche elemento x è in relazione con più elementi y: questo caso è più problematico, tuttavia, a volte, può essere risolto con una restrizione del codominio della funzione, analogamente a quanto fatto prima. In alternativa è necessario rivedere la relazione y=f(x), cambiandola. [Vedi esempio 1]
• Non ha importanza se qualche elemento di y è associato a più elementi x, purchè le coppie ordinate rispettino la relazione y=f(x).

Definizione 2

Dati due insiemi X, Y si definisce funzione da X in Y una relazione r in X × Y tale che sia verificata la seguente espressione: \(f: X → Y, \forall \; x \in X,\; \exists! \; y \in Y \; | \; (x,y) ∈ ℜ \) dove ℜ è il grafico definito dalla relazione r e (x, y) una coppia ordinata definita dal prodotto cartesiano X × Y.

Confrontando le due definizioni precedenti notiamo che le uniche differenze nel linguaggio matematico sono y=f(x) nella prima e (x,y) ∈ ℜ nella seconda. Sostanzialmente entrambe dicono che ogni coppia (x,y) che soddisfa la relazione non può avere in comune con le altre la prima coordinata, l’elemento x.

NOTA: Una funzione, in quanto relazione, è sempre sottoinsieme del prodotto cartesiano tra insieme di partenza e di arrivo, X × Y.

Definizione 3

Dati due insiemi X, Y si definisce funzione la relazione tale per cui la seguente espressione è valida: \(\forall \; x \in X\), l’insieme {\(y ∈ Y | (x,y) ∈ ℜ\)} comprende un unico elemento

Anche questa definizione ribadisce quanto detto al punto precedente rispetto all’unicità della prima coordinata nelle coppie ordinate appartenenti al grafico ℜ della relazione.

NOTA: Queste 3 definizioni sono tra loro analoghe e sono equivalenti ad affermare che date due coppie (x, y), (x, y’) ∈ ℜ, ovvero soddisfacenti la relazione data, si ha che se il primo elemento coincide deve coincidere anche il secondo: \( (x, y), (x, y’) ∈ ℜ ⇒ y = y’ \) e se ciò non si verifica la funzione non è ben definita.

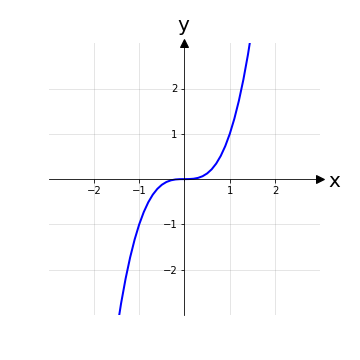
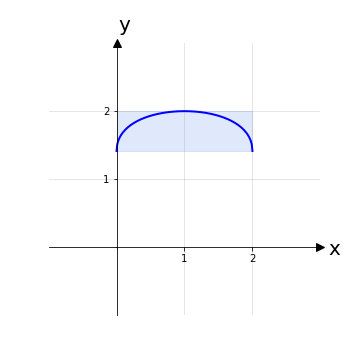
Applicando quanto appreso possiamo dire che il primo grafico è una funzione mentre il secondo no, nemmeno con una restrizione del dominio.

Viene qua proposto un ulteriore esempio, rispetto a quelli esposti nella pagina Funzioni, sfruttando le definizioni alternative elencate in questa pagina.

Esempio 1: Sia X l’insieme ℤ. La relazione X → X | x ⟼ x - 1 ⋀ x ⟼ x + 1, ovvero la relazione che mette in corrispondenza un elemento con il precedente e il successivo non è una funzione. Infatti, per esempio usando la definizione 3, l’insieme {y ∈ Y | (x,y) ∈ ℜ} è composto dai due elementi y₁ = x-1, y₂ = x+1 che sono appunto il precedente e il successivo del numero x. Per esercizio si provi a verificare anche con la definizione 1 e 2 che la relazione data non è una funzione.