Grafico di una funzione

Il metodo più utilizzato per rappresentare graficamente una funzione generica è mediante l’utilizzo del diagramma cartesiano. Qua ci concentriamo principalmente sulle funzioni reali di variabile reale per via delle proprietà dell’insieme ℝ e di ciò che se ne può ricavare; tuttavia quanto detto in questa pagina vale anche per altri insiemi numeri, esclusi i numeri complessi ℂ. 

Richiamiamo per comodità il concetto di grafico di una funzione spiegato più nel dettaglio nella pagina Relazioni binarie e loro grafici.

Il grafico, indicato come ℜ, di una funzione generica, f: X → Y è definito come l’insieme dei punti (x,y) del piano cartesiano tali che x è un elemento del dominio di f e y è l’immagine di x attraverso la relazione che definisce la funzione, ovvero y = f(x). In linguaggio matematico ciò si traduce come segue:

ℜ = {(x,y) ∈ X×Y | y=f(x)}

ricordando che il piano cartesiano è definito come il prodotto cartesiano tra i due insiemi, X x Y.

Nel caso di una funzione reale di variabile reale generica, f: ℝ → ℝ, quanto detto si può scrivere semplicemente come segue:

ℜ = {(x,y) ∈ ℝ²| y=f(x)}

dove ℝ² indica il prodotto cartesiano ℝ x ℝ.  

Nota: Per coerenza con le altre pagine il grafico di una funzione sarà indicato col simbolo ℜ. Tuttavia in diversi testi si può trovare indicato come Gr(f) oppure G_f .

Piano cartesiano

Il piano cartesiano è un sistema di riferimento in cui, fissata un’unità di misura, ogni punto viene individuato da una coppia ordinata le cui componenti sono dette coordinate cartesiane. Esso consiste in due rette orientate ortogonali tra loro, una orizzontale detta ascissa e una verticale detta ordinata, con origine il punto O di intersezione tra le due; tale origine è indicata dalla coppia (0,0).

Per convenzione poniamo come ascissa gli elementi x ∈ X e come ordinata gli elementi y ∈ Y. In generale X e Y coincidono con l’insieme dei numeri reali ℝ e ogni punto del piano rappresenta quindi un elemento del prodotto cartesiano di X × Y, che equivale all’insieme ℝ².

In particolare se l'unità di misura usata sugli assi è equivalente, si dice che il sistema di riferimento è monometrico, altrimenti si dice che è dimetrico.

Di seguito una rappresentazione di un piano cartesiano con sistema di riferimento monometrico, dove l’unità di misura scelta è pari a 1:

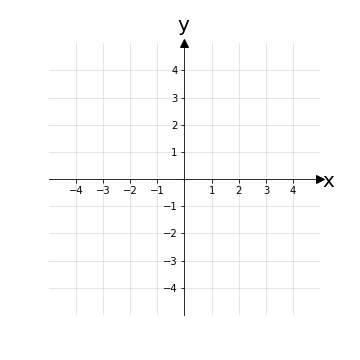
Notiamo che le due rette perpendicolari del piano cartesiano definiscono quattro zone distinte, ciascuna zona prende il nome di quadrante. Convenzionalmente sono numerati dal primo in alto a destra procedendo in senso antiorario fino all’ultimo in basso a destra.

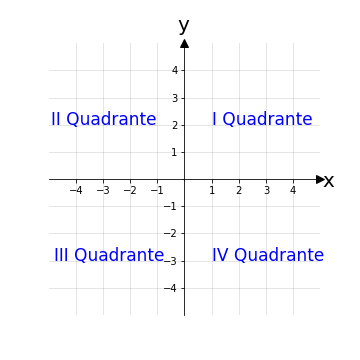
La differenza tra un quadrante e l’altro è dovuta al fatto che:

• tutti i punti del primo quadrante possiedono entrambe le coordinate positive

• tutti i punti del secondo quadrante possiedono l’ascissa negativa e l’ordinata positiva

• tutti i punti del terzo quadrante possiedono entrambe le coordinate negative

• tutti i punti del quarto quadrante possiedono l’ascissa positiva e l’ordinata negativa

Per rappresentare nel piano cartesiano una coppia ordinata (x,y) di numeri reali, altrimenti detto punto del piano cartesiano P(x,y), basta rappresentare il punto P₁(x,0) che corrisponde al valore di x sull’asse delle ascisse e il punto P₂(0,y) che corrisponde al valore di y sull’asse delle ordinate. A questo punto si tracci da P₁ la parallela all’asse y e da P₂ la parallela all’asse x, l’intersezione di tali parallele identifica il punto P(x,y), dove x e y indicano proprio le coordinate cartesiane del punto P.

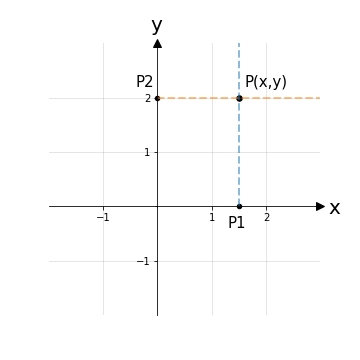
Grafico di una funzione reale di variabile reale

Per rappresentare graficamente una funzione si seguono tre passi fondamentali:

1. Costruzione della tabella dei valori

2. Rappresentazione dei punti corrispondenti

3. Tracciare il grafico della funzione

Per capire meglio i passaggi proviamo a rappresentare un grafico di funzione.

Esempi di grafico di una funzione

1. Consideriamo la funzione data dalla seguente relazione: y = 2x+3 .

La tabella dei valori è composta da due colonne, quella di sinistra per i valori di x e quella di destra per i valori di y. Riempiamo la colonna delle x con dei valori numerici a scelta, possibilmente comodi, e scriviamo nell’altra colonna i corrispondenti valori di y. Per esempio scegliamo i seguenti valori delle ascisse:

Per trovare i corrispettivi valori delle y, dobbiamo risolvere l’equazione della funzione (y=2x+3) per ciascun valore di x. Quindi per il primo valore dobbiamo svolgere f(0), cioè sostituire la variabile x con 0, ovvero y = 2(0) + 3 ottenendo y = 3. 

Ripetendo tale passaggio per ciascun valore di x otteniamo i seguenti valori di y:

2. Trovati alcuni punti, possiamo rappresentarli sul piano cartesiano come visto in precedenza:

   

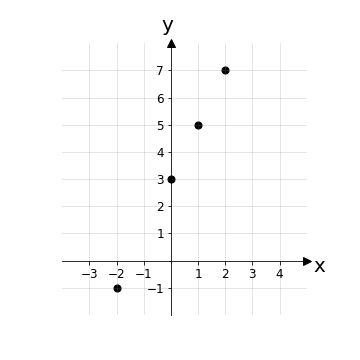
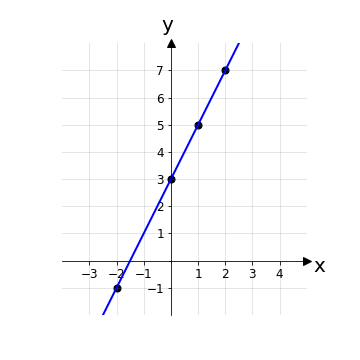
3. Per concludere basta tracciare una retta che attraversi ciascun punto:

   

Attenzione: Questa operazione risulta particolarmente efficace quando il grafico da rappresentare è una retta. Tuttavia spesso i grafici sono più complessi e questo metodo non basta se si vuole rappresentarli “a mano”, a meno di non avere tabelle dei valori lunghissime. L’analisi matematica fornisce gli strumenti per effettuare queste rappresentazioni in modo qualitativo ma relativamente rapido, senza dover ricorrere a un lunghissimo calcolo bruto.

In particolare, nel piano cartesiano, un grafico ℜ è grafico di una funzione solamente se ogni retta verticale, quindi parallela all’asse delle ordinate, x = k, con k ∈ dom(X), interseca il grafico della funzione al massimo in un punto, come visto della definizione di funzione stessa. 

Esempio 1: Considerando il grafico ℜ₁ della funzione y = 2x+3 precedente, possiamo affermare che esso è il grafico di una funzione ben definita: qualsiasi retta verticale parallela all’asse delle ordinate si tracci si avrà sempre un’unica intersezione con ℜ₁.

Esempio 2: Consideriamo la relazione r ≔ "x²+y² = 1" che definisce una circonferenza di raggio unitario e chiamiamo ℜ₂ il suo grafico. Applichiamo il metodo delle rette verticali per verificare se è effettivamente una funzione:

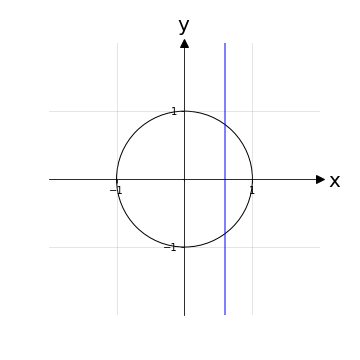
e appare evidente come ci siano 2 intersezioni con ℜ₂ per più rette, o meglio infinite rette, del tipo x = k, con k ∈ (-1,1). Il grafico di una circonferenza non è quindi il grafico di una funzione.