Verifica analitica iniettività funzione

Brevemente, una funzione f: X → Y è detta iniettiva se ogni elemento di Y ha al massimo una controimmagine in X.

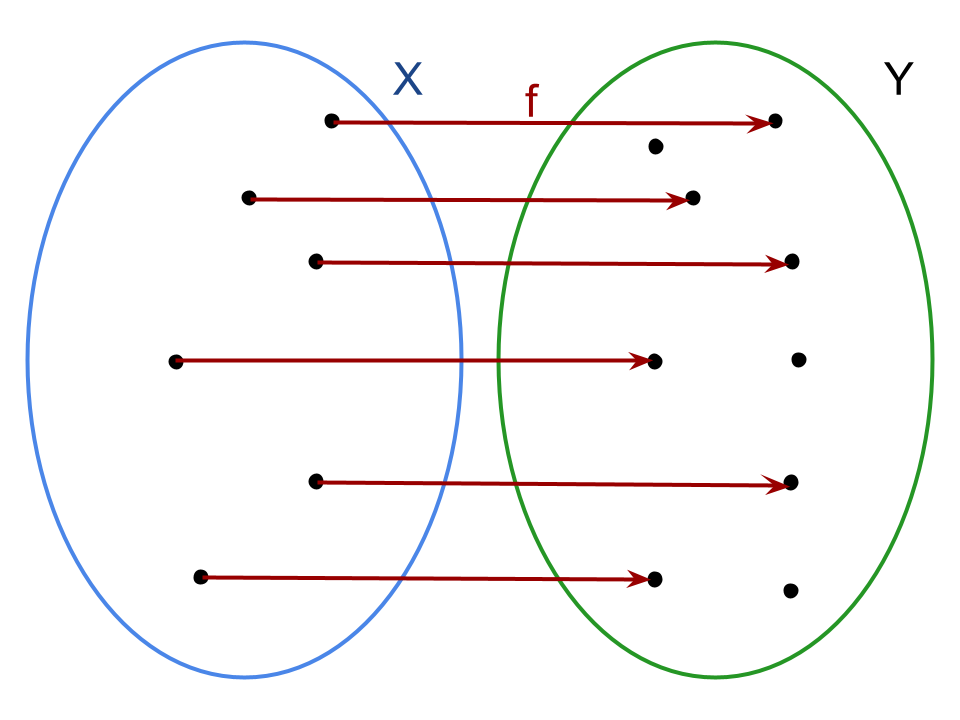
In linguaggio matematico diremo che un’applicazione f: X → Y è iniettiva se è verificato che ∀ x₁, x₂ ∈ X | f(x₁) = f(x₂) ⇒ x₁ = x₂ovvero x₁ e x₂ coincidono se l’immagine dei due elementi è la stessa.

Come mostrato in funzioni iniettive, nel caso più comune di funzioni reali di variabile reale esiste un metodo grafico per verificare questa proprietà: si traccino delle rette orizzontali y = k, con k ∈ ℝ, e si verifichi che tutte queste rette intersecano al massimo una volta il grafico della funzione.

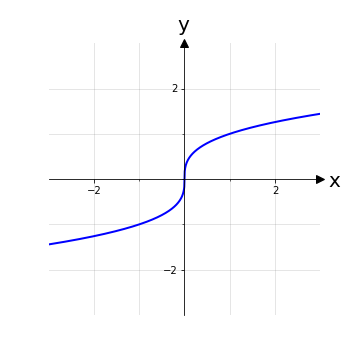
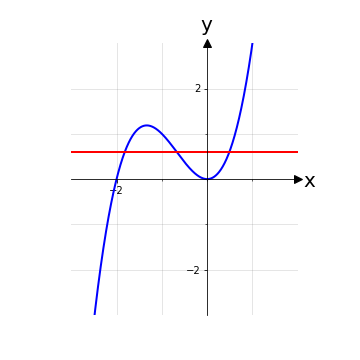
Tuttavia questo metodo richiede una non banale capacità di disegnare, almeno qualitativamente, il grafico di una funzione. Per questo motivo di seguito si illustra un metodo analitico che, nel caso di espressioni relativamente semplici, è altrettanto efficace nel verificare l’iniettività o meno di una funzione.

Metodo analitico

Sia data una funzione, reale di variabile reale, y = f(x). Partendo dalla definizione di iniettività, cioè ∀ x₁, x₂ ∈ X | f(x₁) = f(x₂) ⇒ x₁ = x₂, il procedimento da seguire è evidente:

• si impone l’uguaglianza f(x₁) = f(x₂), dove x₁, x₂ sono due punti generici
• con le solite regole algebriche risolviamo l’equazione esprimendo x₁ in funzione di x₂ o viceversa
• controllare se è verificata o meno l’uguaglianza x₁ = x₂

Se alla fine il risultato è x₁ = x₂ allora la funzione è iniettiva mentre, se l’equazione ammette più soluzioni, la funzione non è iniettiva.

Esempio 1: f: ℝ → ℝ, x ⟼ f(x) con f(x) ≔ x
Altrimenti detta funzione identità questo è un caso banale, poiché è evidente che la definizione di iniettività è soddisfatta:f(x₁) = f(x₂)x₁ = x₂

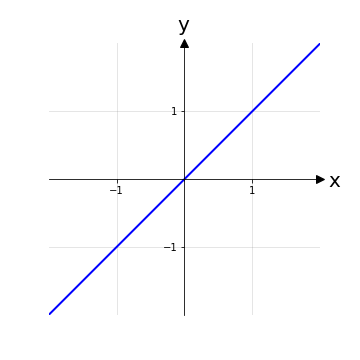
NOTA: Questo risultato è generalizzabile per tutte le funzioni polinomiali dove compaiono solo termini con potenza ad esponente dispari.

Esempio 2: g: ℝ → ℝ⁺, x ⟼ g(x) con g(x) ≔ x²
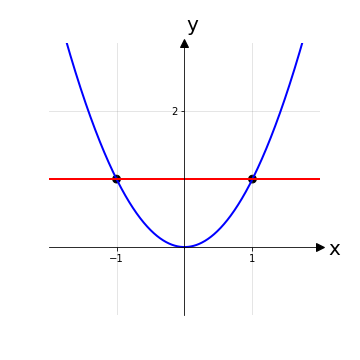
La legge della funzione g è quella che descrive una parabola quindi si può già intuire che non sia iniettiva. Per verificarlo scriviamo\(g(x_1) = g(x_2)\)\(x_1^2 = x_2^2\)\(\sqrt{x_1^2}=\sqrt{x_2^2}\)\(±x_1 = ±x_2\)e dato che è ripetitivo il doppio ± possiamo scrivere\(x_1 = ±x_2\)L’equazione ricavata ammette più di una soluzione, in particolare vanno bene tutte le coppie di valori (x₁,x₂), (-x₁,x₂). Risulta evidente che la funzione f non sia iniettiva.

NOTA: Questo risultato è generalizzabile per tutte le funzioni polinomiali dove compaiono anche termini con potenza ad esponente pari.

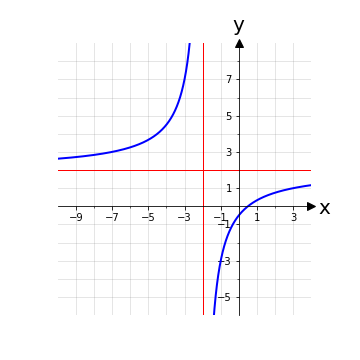
Esempio 3: h: ℝ\{-2} → ℝ, x ⟼ h(x) con h(x) ≔ \(\frac{2x-1}{x+2}\)
La legge della funzione h è del tipo polinomiale e, in generale, si può dedurre l’iniettività se non compaiono termini con potenza ad esponente pari come visto negli esempi sopra.\(h(x_1) = h(x_2)\)\(\frac{2x_1-1}{x_1+2} = \frac{2x_2-1}{x_2+2}\)e, dato che abbiamo escluso -2 dal dominio, possiamo continuare con\((2x_1-1)(x_2+2) = (2x_2-1)(x_1+2)\)\(2x_1x_2 - x_2 + 4x_1 - 2 = 2x_2x_1 - x_1 + 4x_2 - 2\)\(5x_1 = 5x_2\)\(x_1 = x_2\)La funzione h è quindi iniettiva.

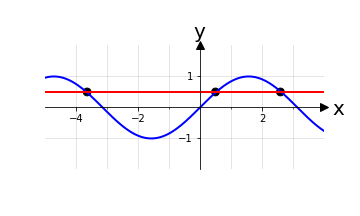
Esempio 4: t: ℝ → [-1,1], x ⟼ t(x) con t(x) ≔ sin(x)
La funzione seno è una funzione periodica e, in quanto tale, non può essere iniettiva.\(t(x_1) = t(x_2)\)\(sin(x_1) = sin(x_2)\)Questa equazione è verificata ∀ x₁ | x₁ = x₂ + 2n𝜋, n ∈ ℤ.

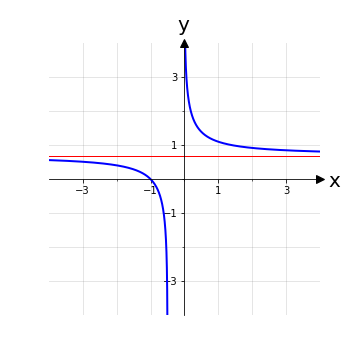
Esempio 5: s: Dom(s) → ℝ, x ⟼ s(x) con s(x) ≔ \(ln(\frac{2x+1}{x})\)
La legge della funzione s è un logaritmo di base e, altrimenti detto logaritmo naturale. Questo tipo di funzione, se l’argomento tra parentesi è semplicemente la variabile x, è monotona stretta, ossia è una funzione che cresce solamente (come y = x) o decresce solamente (come y = -x). Una funzione di questo tipo si può intuire essere iniettiva, tuttavia è importante valutare l'argomento del logaritmo: infatti a seconda dell’argomento la funzione complessiva potrebbe non essere iniettiva.

Prima di procedere, tuttavia, dobbiamo trovare il dominio naturale della funzione: sia la frazione che il logaritmo potrebbero richiedere delle condizioni di esistenza. In particolare la frazione con x al denominatore porta ad escludere il valore x = 0, mentre il logaritmo richiede che il suo argomento sia strettamente maggiore di 0, cioè \(\frac{2x+1}{x}\) > 0.
Non essendo il focus della pagina si risparmia sui conti prendendo il seguente risultato per buono. In caso di dubbi, si invita a provare a risolvere la disequazione.
Dom(s) ≔ {x ∈ ℝ | x>0 ⋁ x< -1/2}

Procediamo imponendo la solita uguaglianza:\(s(x_1) = s(x_2)\)\(ln(\frac{2x_1+1}{x_1}) = ln(\frac{2x_2+1}{x_2})\)
e, a questo punto, siano entrambi i membri esponenti di e. L’operazione è lecita, non avendo la funzione esponenziale condizioni di esistenza sull’esponente, e avendo già determinato il Dom(s) dove l’equazione sopra è ben definita.\(e^{ln(\frac{2x_1+1}{x_1})} = e^{ln(\frac{2x_2+1}{x_2})}\)\(\frac{2x_1+1}{x_1} = \frac{2x_2+1}{x_2}\)\((2x_1+1)x_2 = (2x_2+1)x_1\)\(2x_1x_2+x_2 = 2x_2x_1+x_1\)\(x_2 = x_1\)
Quindi la funzione s è iniettiva sul suo dominio Dom(s).

Per esercizio si provi a verificare se con un altro argomento nel logaritmo la funzione è ancora iniettiva, ad esempio la funzione k: ℝ\{0} → ℝ, x ⟼ k(x) con k(x) ≔ ln(x²).

NOTA: Si ricordi che molte funzioni non iniettive sul loro dominio naturale possono diventarlo con una opportuna restrizione del dominio.