Dominio di una funzione

Tendenzialmente, data una espressione analitica di una funzione f, non viene specificato il suo dominio e il suo codominio: di conseguenza, si assume per convenzione che il dominio naturale di una funzione y=f(x) sia l’insieme di tutti valori reali che si possono assegnare alla variabile indipendente x per i quali esiste il corrispondente valore reale y. In altre parole sono considerate tutte le coppie ordinate con coordinate reali che soddisfano la relazione che definisce la funzione.

Il dominio naturale di una funzione f è noto anche come campo di esistenza di f e può essere ricavato dall’espressione analitica di f; il campo di esistenza di f è sostanzialmente il più grande sottoinsieme di ℝ, anche ℝ stesso, in cui l’espressione analitica della funzione è ben definita.

Osservazione: Due funzioni f e g si definiscono uguali se hanno lo stesso dominio X e se f(x) = g(x) per ogni \( x \in X\).

Restrizione del dominio

Data una funzione f, per particolari operazioni o applicazioni, ad esempio la composizione di funzioni, può essere necessario restringere f.

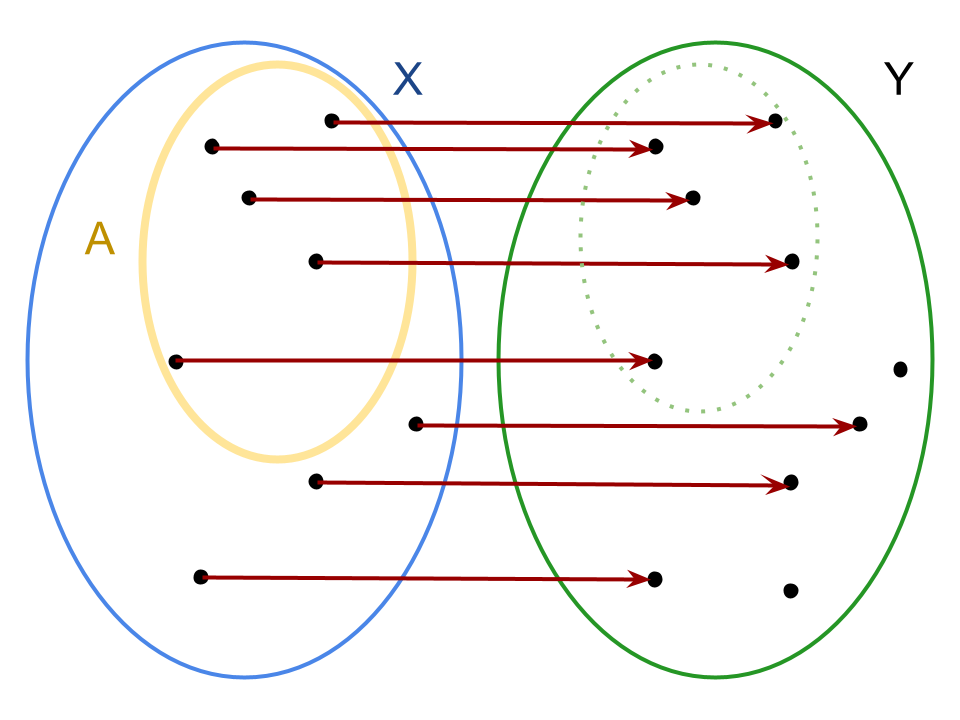
Sia f: X → Y | x ⟼ f(x) e A\(\; \subseteq \; \)X. La restrizione di f ad A è la funzione F_|A: A → Y | x ⟼ f_|A(x), dove f_|A(x) = f(x), \( \forall \; x \in A \). Praticamente una restrizione di una funzione corrisponde ad una restrizione del suo dominio: da X passiamo a un suo sottoinsieme A.

Dominio di funzioni algebriche

Come già visto nella classificazione delle funzioni, le funzioni algebriche possono essere suddivise in due principali classi: funzioni razionali e irrazionali, che a loro volta possono essere intere o frazionarie a seconda se l’incognita compare o meno a denominatore.
La determinazione del dominio di una funzione algebrica si basa sul tipo di classe di appartenenza della funzione, in particolare distinguiamo quindi tra:

• funzioni razionali intere: es. \(f(x)=x^5-3x^3+x^2-5x+7\) dette anche funzioni polinomiali, in cui il dominio è l’insieme ℝ.
• funzioni razionali fratte: es. \(f(x)=\frac{5x}{x+7}\) il loro dominio è l’insieme ℝ meno i valori che rendono nullo il denominatore, ovvero i valori per i quali l’operazione di divisione non ha significato.
• funzioni irrazionali intere: es. \(f(x)=\sqrt[3]{x+3}-5\sqrt{x}+7\) se l’indice della radice è un numero dispari, il dominio della singola radice è banalmente l’insieme ℝ. Se, invece, l’indice della radice è un numero pari, il dominio della singola radice è l’insieme ℝ meno l’insieme dei valori che rendono negativo il radicando. Il dominio della funzione sarà l’intersezione di tutti i domini delle singole radici.
• funzioni irrazionali fratte: es. \(f(x)=\frac{5x}{\sqrt{x}+7}\) come per le funzioni irrazionali intere bisogna prestare attenzione all’indice di ogni radice presente. Inoltre, come visto per le funzioni razionali fratte, si deve imporre che il denominatore della divisione sia diverso da 0, escludendo dal dominio i valori per cui tale condizione non è verificata.

In sintesi, per determinare il dominio di una funzione algebrica occorre verificare che:

• Gli eventuali denominatori siano sempre diversi da zero, o non nulli
• I radicandi delle eventuali radici di indice pari, siano maggiori o uguali a zero, o non negativi.

Dominio di funzioni trascendenti

• Funzioni logaritmiche: es. \(f(x)=log(x)-log(x+2)\) dopo essersi assicurati che la base del logaritmo sia maggiore di 0 e diversa da 1, occorre imporre che l’argomento del logaritmo sia strettamente maggiore di 0, ovvero positivo.
• Funzioni goniometriche: es. \(f(x)=sin(x)\), \(\quad g(x)=cos(x)\), \(\quad h(x)=tan(x)\) le funzioni goniometriche non hanno problemi di dominio se non nel caso in cui sia presente un’operazione di divisione. In quel caso, come per le funzioni algebriche fratte si deve imporre che il denominatore sia non nullo. Funzioni come sin(x), cos(x) hanno quindi come dominio ℝ mentre funzioni come tan(x), cot(x) avranno dei valori esclusi dal dominio in quanto tali funzioni sono rispettivamente definite come \(\frac{sin(x)}{cos(x)}\) e \(\frac{cos(x)}{sin(x)} \).
• Funzioni esponenziali con base costante: es. \(f(x)=e^{x-3}\) a patto che la base sia non negativa il dominio di queste funzioni è l’insieme ℝ.
• Funzioni esponenziali con base variabile: es. \(h(x)=f(x)^{g(x)}=x^{x+2}\) come nel caso precedente occorre imporre che la base f(x) sia non negativa e che l’esponente sia strettamente positivo per x₀ | f(x₀) = 0. Le condizioni da imporre sono quindi:
  • f(x) \(\ge\) 0
  • se ∃ x₀ ∈ ℝ | f(x₀) = 0 ⇒ g(x₀) > 0, altrimenti x₀ ∉ Dom(f)
• Funzioni goniometriche inverse: es. \(f(x)=arcsin(x)\), \(\quad g(x)=arccos(x)\), \(\quad h(x)=arctan(x)\) mentre la funzione arctan(x) ha come dominio ℝ, le funzioni arcsin(x) e arccos(x) devono avere l’argomento - l’espressione tra parentesi - compreso tra -1 e 1, estremi compresi. In questo specifico caso l’argomento è x e quindi il dominio di entrambe le funzioni sarà dato dall’insieme [-1,1].
  
  

  NOTA: Queste funzioni sono state citate per completezza ma qui non ci soffermiamo sui motivi specifici.

NOTA: Nel caso della compresenza di più “operazioni critiche” nella funzione di cui vogliamo ricavare il campo di esistenza, occorre stabilire il dominio per ogni singola funzione/operazione e poi intersecare tutti i domini trovati per ottenere il dominio della funzione di partenza.

Esempi

Determinare i domini delle seguenti funzioni:

1. \(\quad y=x^2-3 \)
2. \(\quad y=\frac{1}{2x^3}+4x \)
3. \(\quad y=\sqrt{2x}+\sqrt[3]{x-5}\)
4. \(\quad y=\frac{1}{\sqrt{5x+1}}\)
5. \(\quad y=log(x-3)\)
6. \(\quad y=tan(x)\)
7. \(\quad y=sin(x^2)\)
8. \(\quad y=x^{x+2}\)

1. La funzione è definita \( \forall\; x \in ℝ\) e di conseguenza il dominio della funzione è l’insieme ℝ
2. Si noti che si ha una funzione fratta poiché è presente la variabile indipendente anche al denominatore. In questo caso di deve imporre le condizioni di esistenza, ossia che il denominatore della frazione sia diverso da zero: 2x³ ≠ 0 ⇒ x³ ≠ 0 ⇒ x ≠ 0
   Il dominio della funzione è quindi definito \( \forall x \in ℝ \) | x ≠ 0, o analogamente come \((-\infty, 0)\) U \((0, +\infty)\).
3. Notiamo che nella funzione ci sono due radici con la variabile indipendente al radicando; però la seconda radice ha indice dispari e di conseguenza non ci sono limitazioni ai valori che può assumere x. Basta solo porre la condizione che il radicando della prima radice, radice di indice pari, sia maggiore o uguale a zero: \(2x \ge 0\) => \(x \ge 0\). Il dominio della funzione è semplicemente definito \( \forall\; x \in R\; |\; x ≥ 0\).
4. In questo caso si ha una radice di indice pari al denominatore e si devono quindi soddisfare due condizioni:
   • denominatore della frazione diverso da 0
   • radicando non negativo
   Se il radicando fosse zero (seconda condizione soddisfatta) il denominatore diventerebbe 0, il che non è accettabile. Per risolvere questo esercizio il radicando deve essere strettamente maggiore di zero: 5x+1 > 0 ⇒ x > \( -\frac{1}{5}\). Il dominio è quindi definito \( \forall x \in ℝ \; | \; x >- \frac{1}{5} \).
5. In quanto funzione logaritmica si impone semplicemente che l’argomento del logaritmo sia strettamente maggiore di 0: x-3 > 0 ⇒ x > 3 e quindi il dominio corrisponde all’insieme reale \((3, \infty)\).
6. Come detto nel paragrafo “Dominio delle funzioni trascendenti” le funzioni goniometriche non hanno problemi di dominio se non nel caso in cui si presenti una divisione. In questo caso \( tan(x)= \frac{sin(x)}{cos(x)}\) e si deve quindi escludere dal dominio i valori per cui cos(x)=0; essendo il coseno una funzione periodica i cui valori oscillano in [-1,1] i valori da escludere dal dominio saranno infiniti, ma con una certa periodicità: cos(x)=0 ⇔ \(x =\frac{𝜋}{2}+k𝜋\), con k ∈ ℤ. Il dominio della funzione tangente sarà dunque definito ∀ x ∈ ℝ | x ≠ \(\frac{𝜋}{2}+k𝜋\), k ∈ ℤ.
7. La funzione sin è ben definita su tutto ℝ: eventuali problemi possono essere al massimo dovute all’argomento di sin. Essendo l’argomento un semplice polinomio - x²- non si riscontra nessuna criticità e si può quindi affermare che il dominio naturale della funzione coincide con ℝ.
8. La funzione è del tipo \(f(x)^{g(x)}\)con base ed esponente variabili. Noto che una potenza (a esponente reale), per essere ben definita, deve avere base non negativa si impone f(x)≥ 0 ⇒ x ≥ 0. Sarebbe però un errore concludere che il dominio della funzione sia l’insieme \((0, \infty)\) senza aver prima controllato un caso particolare: nel caso in cui la base sia pari a 0 occorre che l’esponente sia strettamente maggiore di 0 per non incorrere nella forma indeterminata 0⁰ oppure nella non definita frazione con denominatore nullo es. \(0^{-1}= \frac{1}{0}\). In questo caso l’esponente x+2 > 0, ∀ x ∈ ℝ | x > 0 e quindi l’insieme \((0, \infty)\) è proprio il dominio della funzione.