Come trovare il campo di esistenza di una funzione

Nella pagina dominio di una funzione sono state evidenziate le criticità delle più comuni funzioni e il modo di trattarle. Qua si vogliono riassumere i ragionamenti principali da fare per calcolare il campo di esistenza, o dominio naturale, di una generica funzione di cui sia nota la legge analitica e fornire qualche strumento operativo grafico per ridurre possibili errori.

Sia quindi data la legge analitica della funzione \( f(x)=log(\frac{1}{x-3}) \cdot \sqrt{x-1}\)

i passaggi principali da svolgere sono i seguenti:

1° passaggio

Si ricercano nella legge analitica tutte le operazioni critiche:

• divisioni
• radici di indice pari
• logaritmi
• esponenziali con base variabile
• funzioni goniometriche inverse

Su queste operazioni imponiamo le condizioni di esistenza affinché tali operazioni siano definite, come visto appunto in dominio di una funzione:

• \( \frac{1}{x-3} ⇒ x - 3 ≠ 0\)
• \( log( \frac{1}{x-3} ) ⇒ \frac{1}{x-3}>0 \)
• \( \sqrt{x-1} ⇒ x-1 ≥ 0\)

2° passaggio

Dato che tutte le condizioni precedentemente imposte devono valere contemporaneamente si andrà a risolvere un sistema di N disequazioni, con N pari al numero di operazioni critiche. Scritto il sistema procediamo risolvendo tutte le disequazioni: \( \begin{equation} \left\{\begin{array}{@{}l@{}l@{}} x - 3 \neq 0 \Rightarrow x \neq 3\\ \frac{1}{x-3} > 0 \Rightarrow x - 3 > 0 \Rightarrow x > 3\\ x - 1 \geq 0 \Rightarrow x \geq 1 \end{array}\right.\, \end{equation} \)

NOTA: Nonostante il risultato di alcune disequazioni possa tranquillamente essere scartato in quanto ripetitivo si consiglia di non bruciare le tappe, almeno per i primi esercizi.

3° passaggio

Per visualizzare facilmente l’operazione di intersezione tra gli insiemi risultanti dalle disequazioni procediamo tracciando una retta orizzontale orientata, indicata come asse x in analogia all’asse del piano cartesiano associato al dominio della funzione. Al di sotto di tale retta si traccino tante rette quante sono le N disequazioni del sistema e su di esse si riportino i risultati trovati nel II passaggio. Infine basta osservare per quali valori di ℝ tutte le rette sono caratterizzate contemporaneamente da una soluzione: l’insieme di questi valori che soddisfano il sistema del II passaggio è proprio il dominio naturale della funzione studiata. Completiamo quindi l’esempio graficando quanto segue:

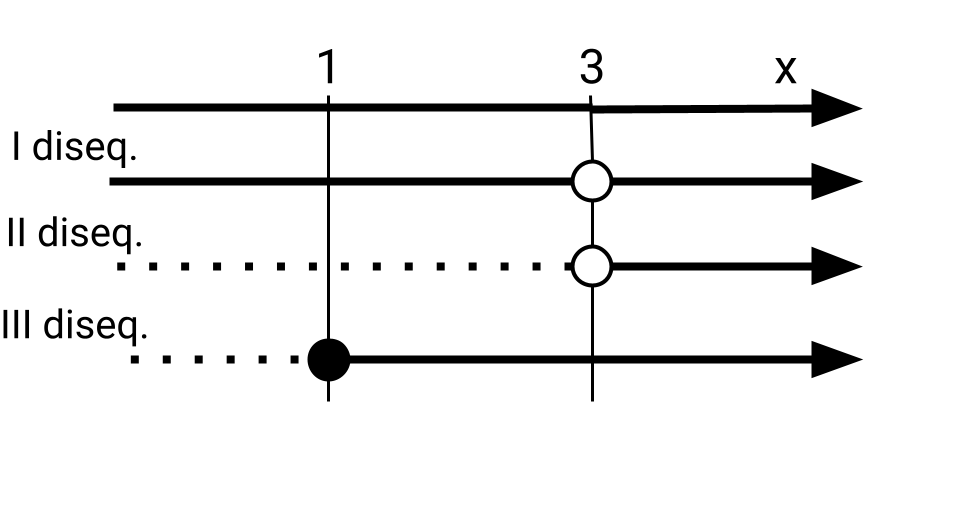
In questo caso con una linea continua abbiamo indicato i valori ammessi dalle singole condizioni imposte, mentre con una linea tratteggiata i valori che non sono accettabili. In particolare, si noti come per le prime due disequazioni compaia un pallino vuoto, notazione che indica l’esclusione di quel valore (3), mentre nella terza compare un pallino pieno, convenzione che indica l’ammissione di quel valore (1). Infine confrontiamo tutte le rette tracciate e troviamo il dominio della nostra f(x) come intersezione di tutti i valori ammissibili.
In questo caso il dom(f) ≔ {x ∈ ℝ | x > 3} che riportiamo anche in figura in colore rosso: