Funzioni pari e funzioni dispari

Data una funzione f: A ⊆ ℝ → ℝ,  dove A ne è il dominio, abbiamo che:

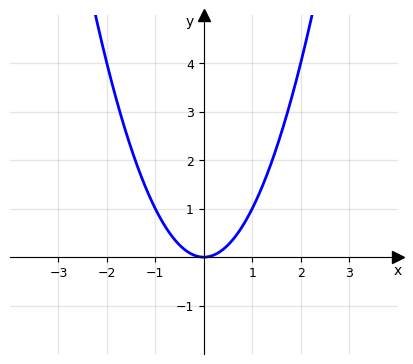
• f è una funzione pari se ∀ x ∈ A anche -x ∈ A e vale che f(-x) = f(x), ∀ x ∈ A. Equivalentemente, si può dire che la funzione assume valori simmetrici rispetto all’asse delle ordinate y.

  

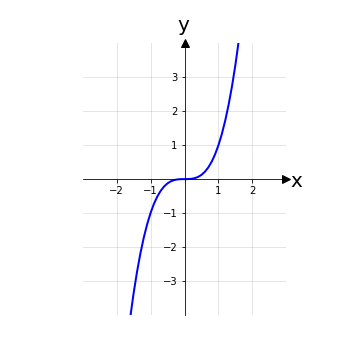
• f è una funzione dispari se ∀ x ∈ A anche -x ∈ A e vale che -f(-x) = f(x), ∀ x ∈ A. Equivalentemente, si può dire che la funzione assume valori simmetrici rispetto all’origine del piano cartesiano.

  

• f non è né pari né dispari se ∃ x ∈ A | -x ∉ A ⋁ {f(x) ≠ f(-x) ⋀ f(x) ≠ -f(-x)}. Equivalentemente, si può dire che basta un controesempio che falsifichi la parità e un controesempio che falsifichi la disparità.

  

Nota: Prima di verificare le varie condizioni sulla f(x), è importante assicurarsi della simmetria del dominio rispetto allo zero ovvero della condizione ∀x ∈ A ⇒ -x ∈ A. Se un dominio non è simmetrico rispetto all’origine, la funzione definita su quel dominio sarà sicuramente non pari e non dispari.

Alcune proprietà delle funzioni pari e dispari

Sia dato un dominio A ⊆ ℝ simmetrico rispetto all’origine e siano date quattro funzioni su di esso definite: 

f: A → ℝ e g: A → ℝ, entrambe pari

h: A → ℝ e t: A → ℝ, entrambe dispari

Seguono le seguenti proprietà di somma:

1. f+h: A → ℝ, ossia la somma di una funzione pari e una dispari, in generale non è nè pari nè dispari.

2. f+g: A → ℝ, ossia la somma di due funzioni pari, è a sua volta una funzione pari.

3. h+t: A → ℝ, ossia la somma di due funzioni dispari, è sempre una funzione dispari.

Nota: Tali proprietà valgono anche per l’operazione di sottrazione: infatti, la sottrazione non è altro che la somma dell’opposto. Opposto che si ottiene moltiplicando per c = -1 la seconda funzione e, come vedremo nelle proprietà 1. e 2. che seguono, tale operazione conserva la parità e la disparità.

Seguono inoltre le seguenti proprietà per il prodotto:

1. ∀c ∈ ℝ \ {0}, c\( \cdot \)f: A → ℝ, ossia il prodotto di un numero per la funzione pari, è ancora una funzione pari.

2. ∀c ∈ ℝ \ {0}, c\( \cdot \)h: A → ℝ, ossia il prodotto di una costante per una funzione dispari, è a sua volta una funzione dispari.

3. f\( \cdot \)h: A → ℝ, ossia il prodotto tra una funzione pari e una dispari, è sempre una funzione dispari.

4. f\( \cdot \)g: A → ℝ, ossia il prodotto tra due funzioni pari, è ancora una funzione pari.

5. h\( \cdot \)t: A → ℝ, ossia il prodotto tra due funzioni dispari, risulta essere una funzione pari.

Nota: Le ultime 3 proprietà valgono anche per l’operazione di divisione purché il divisore, ossia la funzione a denominatore, sia diversa da 0 in ogni suo punto:

siano date due generiche funzioni f,g: A ⊆ ℝ → ℝ, entrambe pari, entrambe dispari o una pari e una dispari; nell’eseguire l’operazione \(\frac{f}{g}\) si deve imporre g(x) ≠ 0.

Nel caso in cui qualche punto x ∈ A sia tale che g(x) = 0 (e ciò varrà anche per -x ∈ A) è possibile eseguire comunque l’operazione applicando però delle restrizioni sul dominio A di partenza, sostanzialmente togliendo gli zeri.

Due ultime importanti proprietà sono, data una f: A ⊆ ℝ → ℝ generica:

1. tale funzione f può essere sempre scomposta in una somma tra una funzione pari e una dispari, come \(f(x) = \frac{f(x)+f(-x)}{2}+ \frac{f(x)-f(-x)}{2}\).

2. se f è sia pari che dispari allora è la funzione identicamente nulla f(x) = 0, ∀ x ∈ A.

Per tutte le proprietà elencate è possibile fare una dimostrazione. Di seguito è riportata a titolo di esempio quella dell’ultima proprietà enunciata.

Cenno di prova: Per ipotesi sappiamo che  f: A ⊆ ℝ → ℝ è sia pari che dispari, ovvero che ∀x ∈ A, f(x) = f(-x) ⋀ f(x) = -f(-x). Allora si ha che f(-x) = -f(-x), ossia un dato elemento deve essere uguale al suo opposto, ma ciò è vero se solo se f(-x) = 0. Dato che deve valere per ogni punto del dominio, allora f(x) = 0 ∀x ∈ A, che è la funzione identicamente nulla.

Nota: Nell’elencare le proprietà si è voluta mantenere una certa generalità. Tuttavia il caso più utile in cui si possono utilizzare tali proprietà sono nelle funzioni reali di variabile reale, ossia gli insiemi X e Y generici utilizzati in precedenza diventano X ≔ ℝ, Y ≔ ℝ .

Esempi di funzioni pari e funzioni dispari

Determinare se le seguenti funzioni sono pari, dispari o non presentano simmetrie:

1. y = x²

2. \(y = \frac{1}{(2x^3)}\)

3. y = |x|

4. y = x⁵-2

Per determinare se una funzione è pari o dispari basta applicare le definizioni che sono rispettivamente f(x) = f(-x) e f(x) = -f(-x).

1. Osserviamo che f(x) = x²  mentre f(-x) = (-x)² = (-1)²(x)² = x², quindi abbiamo che f(x) = f(-x) = x² e di conseguenza la funzione è pari. Dato che non è identicamente nulla sicuramente non sarà anche dispari.

2. Abbiamo che \(f(x) = \frac{1}{(2x^3)}\) mentre \(f(-x) = \frac{1}{(-2x)^3}\) = \(\frac{-1}{(2x^3)}\), quindi la funzione non è pari, ma facilmente si può notare che la funzione è dispari, infatti \(f(x) = -f(-x) = \frac{1}{(2x^3)}\).

3. Osserviamo che f(x) = |x| mentre f(-x) = |-x| = |x|, in quanto il modulo considera il valore assoluto, quindi la funzione è pari. Dato che non è identicamente nulla sicuramente non sarà anche dispari.

4. Osserviamo che f(x) = x⁵-2 mentre f(-x) = (-x)⁵-2 = -x⁵-2, quindi la funzione non è sicuramente pari. Verifichiamo se è dispari: notiamo che -f(-x)=x⁵+2 f(x)=x⁵-2 e di conseguenza la funzione è nemmeno dispari, quindi non presenta simmetrie.