Esempi sul calcolo del segno di una funzione

In riferimento alla pagina Zeri e segno di una funzione aggiungiamo qua ulteriori esempi di calcolo, soprattutto nel caso di funzioni trascendenti. Nel caso non si avessero ben chiare quali siano le funzioni trascendenti si può consultare la pagina Classificazione delle funzioni.

Determinare il segno della seguente funzione irrazionale (il cui dominio è il dominio naturale):

1. \(y=\sqrt{x^3-4x}\)

e determinare il segno delle seguenti funzioni trascendenti (il cui dominio è il dominio naturale):

2. \(y=sin(x)\)
3. \(y=ln(x-5)\)
4. \(y=e^x-1\)
5. \(y=x^{3x}-e^x\)

Per determinare il segno che la funzione assume al variare dei punti del dominio basta quindi risolvere una delle due disequazioni, f(x) ≥ 0 o f(x) ≤ 0, e trovare il caso opposto facendo il complementare dell’insieme trovato rispetto a tutto il dominio della funzione.

1. Data \(f(x)=\sqrt{x^3-4x}\) risolviamo la disequazione f(x) ≥ 0. Abbiamo a che fare con una funzione irrazionale dove la variabile indipendente x compare come radicando di una radice pari: per le condizioni di esistenza della funzione radice pari si deve imporre il radicando non negativo cioè \(x^3-4x\ge0\) ⇔ \(x(x^2-4) \ge 0\) ⇔ \(x(x-2)(x+2) \ge0\)
   Dato che la funzione radice pari è una funzione del tipo f: ℝ ⊇ A → ℝ⁺ ci aspettiamo che, dove è definita, la funzione abbia segno positivo. Il problema si riduce quindi alla disequazione sopra dove compaiono 3 termini moltiplicati tra loro: il segno del radicando è dato dal prodotto dei segni di questi 3 termini N₁, N₂, N₃ nell’ordine.
   
   Risolviamo le singole disequazioni del tipo N_i ≥ 0, con i = {1,2,3} e riportiamo i risultati in tabella per effettuare i prodotti dei segni:
   
   La soluzione della disequazione che impone la condizione di esistenza per la funzione radice pari è l’insieme {x ∈ ℝ | -2 ≤ x ≤ 2 ⋁ x ≥ 2} che è proprio il dominio naturale della funzione. Tale funzione è quindi positiva ovunque sul suo dominio e ha tre zeri in x₁ = 0, x₂ = -2, x₃ = 2; nel resto del dominio avrà segno negativo.
   
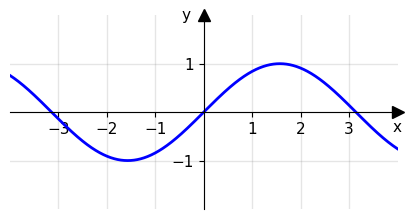
2. Data f(x) = sin(x) risolviamo la disequazione f(x) ≥ 0 sul dominio della funzione che coincide con ℝ. A causa della periodicità 2𝜋 della funzione seno quello che succede è che la funzione ha infiniti zeri per i punti x_i = k𝜋 con k ∈ ℤ interi. Per lo stesso motivo anche il segno della funzione continuerà a cambiare muovendosi lungo il dominio: è perciò necessario il parametro k per identificare tutte le variazioni.
   Dando per nota la conoscenza di questa funzione “base” l’insieme delle soluzioni di f(x) ≥ 0 è l'insieme f⁺ ≔ {x ∈ ℝ | 2k𝜋 ≤ x ≤ 𝜋 + 2k𝜋, k ∈ ℤ} e, in modo complementare, le soluzioni per f(x) < 0 saranno tutti gli elementi dell’insieme ℝ \ f⁺ = {x ∈ ℝ | 2k𝜋 + 𝜋 < x < 2𝜋 + 2k𝜋, k ∈ ℤ}.
   
3. Data f(x) = ln(x-5) risolviamo la disequazione f(x) ≥ 0, ma prima bisogna imporre la condizione di esistenza della funzione logaritmo: x - 5 > 0 ⇔ x > 5 Procediamo risolvendo la disequazione e usiamo la definizione di logaritmo: log_a[ f(x) ] = b ⇔ f(x) = a^b ln(x-5) ≥ 0 ⇔ x-5 ≥ e⁰ ⇔ x-5 ≥ 1 ⇔ x≥6 Quindi la soluzione per f(x) ≥ 0 è l’insieme f⁺ ≔ {x ∈ ℝ | x ≥ 6} e analogamente \(f_- ≔ Dom(f) \ f^+ = \{x ∈ ℝ\; |\; 5 < x < 6\}\).
   

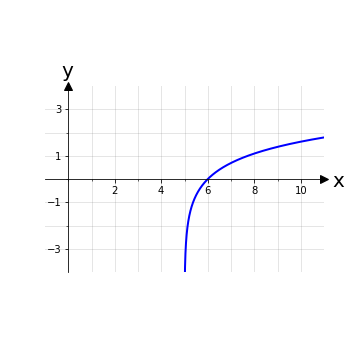
   NOTA: Conoscendo a priori la forma della funzione ln(x) si sarebbe potuta fare una valutazione grafica pensando a ln(x-5) come a ln(x) traslato verso destra di 5 unità.

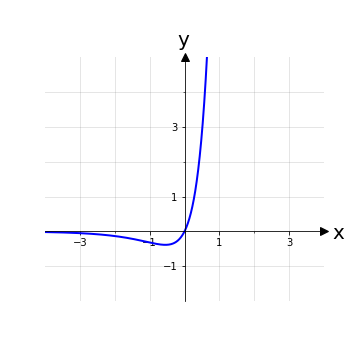
4. Data f(x) = e^x-1 ne determiniamo il segno risolvendo f(x) ≥ 0. Si noti che la funzione esponenziale non presenta punti critici e quindi il dominio naturale è quello dei numeri reali. La disequazione che ci troviamo a risolvere si può riportare nella forma di una disequazione esponenziale elementare del tipo: \( a^{f(x)} \ge b\) con b scrivibile come potenza di base a, ovvero: \( e^x-1 \ge 0\) ⇔ \(e^x \ge 1\) ⇔ \(e^x \ge e^0 \) ⇔ \(x \ge 0\) Quindi la funzione f(x) = e^x-1 è positiva nell’intervallo [0,+∞) con uno zero in x = 0, o equivalentemente f⁺ ≔ {x ∈ ℝ | x ≥ 0}; nel resto del dominio la funzione avrà segno negativo.
   

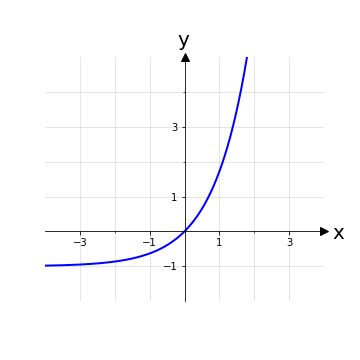
   NOTA:Come per l’esempio del logaritmo, conoscendo a priori la forma della funzione ex si sarebbe potuta fare una valutazione grafica pensando a e^x-1 come a e^x traslato verso il basso di 1 unità.

5. Data f(x) = e^3x-e^x, nel risolvere la disequazione f(x) ≥ 0 ci ritroviamo in un caso molto simile a quello dell’esempio 4), cioè: \(e^{3x}-e^x\ge0\) ⇔ \(e^{3x} \ge e^x\) ⇔ \(3x \ge x\) ⇔ \(4x \ge 0 \) ⇔ \(x \ge 0\) Con la stessa soluzione f⁺ ≔ {x ∈ ℝ | x ≥ 0} dell’esercizio 4).