Zeri e il segno di una funzione
Gli zeri e il segno di una funzione sono informazioni che risultano molto utili durante lo studio della funzione e soprattutto per facilitare la rappresentazione del suo grafico.
Nota: Quanto segue è riferito al comune caso di funzioni reali di variabile reale, tuttavia molti concetti sono estendibili a generiche funzioni g: X → Y.
Sia una funzione f: A ⊆ ℝ → ℝ, determinare il segno di una funzione permette di stabilire, al variare dei valori x del dominio A, la posizione del grafico \(ℜ = {(x,f(x)) \in A \times ℝ }\) della funzione rispetto all’asse delle ascisse.
In particolare distinguiamo tre casi a seconda che il grafico:
stia sopra l’asse delle ascisse, f(x) > 0: per tali valori di x, la funzione viene detta positiva
stia al di sotto dell’asse delle ascisse, f(x) < 0: per tali valori di x, la funzione viene detta negativa
intersechi l’asse delle ascisse, f(x) = 0: per questi valori di x si "annulla" e per questo tali punti vengono chiamati zeri della funzione. In altre parole sono i punti del dominio la cui immagine è 0.
Quindi per determinare gli zeri della funzione basta risolvere l’equazione f(x) = 0 mentre per determinare algebricamente quando una funzione è positiva o negativa, basta risolvere le rispettive disequazioni.
Un trucco per evitare conti ripetitivi può essere quello di risolvere una delle due disequazioni, per esempio f(x) ≥ 0, e, dato l’insieme A1 delle soluzioni trovate, farne il complementare rispetto al dominio A, trovando l’insieme A2 che contiene le soluzioni della disequazione opposta f(x) < 0. I due insieme trovati saranno quindi:
A1 ≔ {x ∈ A | f(x) ≥ 0}
A2 ≔ 𝓒 A1 = A \ A1 = {x ∈ A | f(x) < 0}
e, intuitivamente, non potendoci essere immagini del dominio al di fuori delle 3 categorie sopra elencate, A = A1 U A2 .
Esempi di come determinare il segno di una funzione
Determinare il segno delle seguenti funzioni (il cui dominio è il dominio naturale):
y = x2
y = x2 - 4x + 3
\(y = \frac{x^2+1}{x}\)
Per determinare il segno che la funzione assume al variare dei punti del dominio basta quindi risolvere una delle due disequazioni, f(x) ≥ 0 o f(x) ≤ 0, e trovare il caso opposto facendo il complementare dell’insieme trovato rispetto a tutto il dominio della funzione.
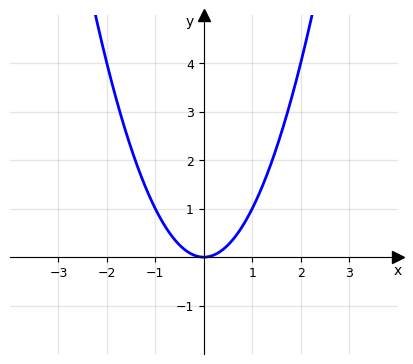
Dato il monomio f(x) = x2 per determinare il segno proviamo a risolvere la disequazione f(x) ≥ 0. Notiamo che il quadrato di un numero reale è sempre un numero positivo a meno che la base non sia 0: avremo quindi
f(x) ≥ 0 ⇔ x2 ≥ 0 verificata ∀x ∈ ℝ
In particolare abbiamo che x0 = 0 è l’unico zero della funzione. Visto che la disequazione f(x) ≥ 0 è verificata su tutto il dominio, la disequazione opposta f(x) < 0 non può avere soluzione: questo significa che la funzione ha segno positivo su tutto il dominio ℝ, con uno zero in x0.
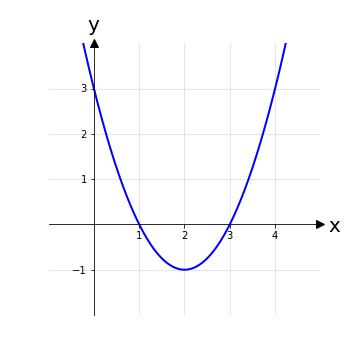
Data f(x) = x2 - 4x + 3 risolviamo, per cambiare, la disequazione f(x) ≤ 0. Per procedere dobbiamo riuscire a scomporre il polinomio: procediamo applicando la scomposizione per somma e prodotto e otteniamo che f(x) = (x -1)(x-3). Gli zeri x1, x2 sono quindi banalmente x1 = 1 e x2 = 3. Dato che il nostro polinomio è una parabola con la concavità verso l’alto (il coefficiente del termine x2 è positivo) la soluzione per f(x) ≤ 0 sarà l’insieme compreso tra i due zeri f_ ≔ {x ∈ ℝ | x ≥ 1 ⋀ x ≤ 3}. In modo complementare la soluzione a f(x) > 0, cioè i valori per cui la funzione ha segno positivo, saranno f+ ≔ ℝ \ f_ = {x ∈ ℝ | x < 1 ⋀ x > 3}.
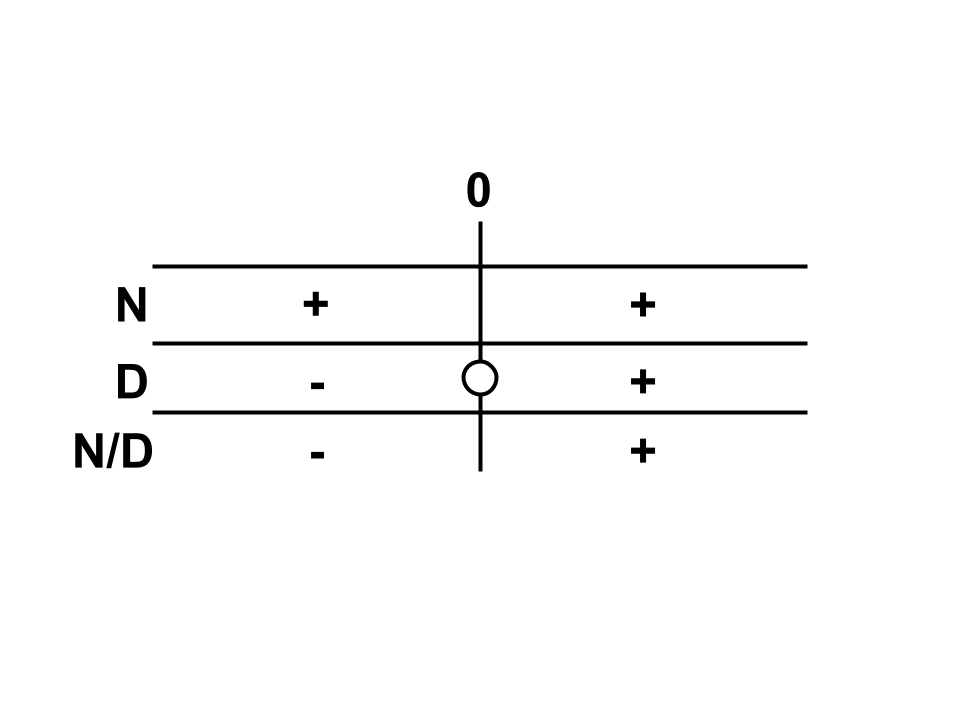
Data la funzione frazionaria \(f(x) =\frac{x^2+1}{x}\) andiamo a risolvere la disequazione f(x) ≥ 0. Intuitivamente il segno della funzione sarà dato dal prodotto del segno del numeratore con il segno del denominatore: la disequazione f(x) ≥ 0 di partenza andrà quindi scomposta nelle due disequazioni N(x) ≥ 0 e D(x) > 0, con N numeratore e D denominatore della funzione in esame.
Si impongono subito le condizioni di esistenza: x ≠ 0; poi si noti come il numeratore sia un polinomio simile a quello dell’esempio a) e quindi N(x) ≥ 0 ∀x ∈ ℝ. Il denominatore è il semplice monomio x che soddisfa x > 0 per le x ∈ ℝ | x > 0.
Mettiamo tutto insieme nella seguente tabella per aiutarci nella visualizzazione delle soluzioni:
Quindi abbiamo ottenuto che f(x) ≥ 0 per f+ ≔ {x ∈ ℝ | x >0} e complementarmente f(x) < 0 per f_ ≔ {x ∈ ℝ | x < 0} come possiamo vedere dal grafico della funzione:
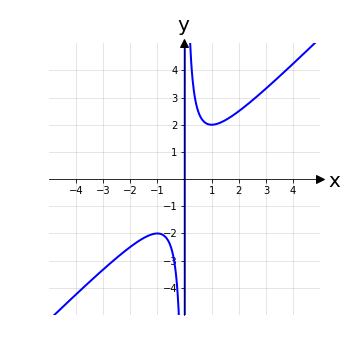
In particolare teniamo a mente che la funzione non ha zeri, cioè non interseca mai l’asse delle ascisse e che in x = 0 non è definita.
Nota: Il metodo di scomporre la disequazione in un sistema di disequazioni poteva essere applicato anche all’esercizio b) dopo aver scomposto il polinomio. In quel caso avremmo avuto due termini al numeratore, N1 = x -1, N2 = x -3, ma il segno della funzione di partenza rimane comunque il risultato del prodotto dei segni dei singoli termini. Indubbiamente, però, nel caso di parabole ax2+bx+c un’osservazione sul segno del coefficiente "a" permette di velocizzare i conti.
Per non allungare troppo il discorso non continuiamo in questa pagina con gli esempi. Tuttavia per guadagnare confidenza nel calcolo del segno di una funzione, soprattutto nel caso di funzioni trascendenti, si consiglia di leggere anche la pagina "Ancora esempi sul calcolo del segno di una funzione".
Gli zeri di una funzione
Una rapida trattazione può essere fatta sul discorso degli zeri di una funzione. In particolare per funzioni reali di variabile reale possiamo individuare diversi tipi di funzioni:
funzioni senza zeri (reali), come il classico polinomio irriducibile x2+1
funzioni con uno o più zeri, ad esempio le più svariate funzioni polinomiali
funzioni con infiniti zeri, come nel caso di funzioni periodiche come sin(x) che spieghiamo come gestire in “Ancora esempi sul calcolo del segno di una funzione
Gli zeri di una funzione, a meno di casi semplici, non sono ricavabili con esattezza con metodi algebrici. In questi casi occorre usare particolari teoremi che si incontreranno più avanti, come il metodo di bisezione che fa uso del teorema degli zeri su cui però non ci soffermiamo ora.
Sempre riguardo gli zeri di una funzione, non si può non citare il Teorema fondamentale dell’Algebra, teorema che garantisce l’esistenza di n zeri (altrimenti detti radici) per un polinomio di grado n. Purtroppo le radici garantite non si trovano tutte nell’insieme ℝ dei reali ma sarà necessario passare al campo dei numeri complessi ℂ per trovarle tutte.