Funzione iniettiva, suriettiva e biettiva

Funzione iniettiva

Una funzione f: X → Y è detta iniettiva se ogni elemento di Y ha al massimo una controimmagine in X; importante è notare la dicitura "al massimo una controimmagine" che si traduce in una condizione che risulta soddisfatta in due casi:

• è ammesso che qualche elemento dell’insieme Y non abbia controimmagine

• nel caso in cui un elemento dell’insieme di arrivo abbia controimmagine quest’ultima deve essere l’unica

In linguaggio matematico, quindi, diremo che un’applicazione f: X → Y è iniettiva se è verificato che:

x₁,x₂ ∈ X | x₁ ≠ x₂ ⇒ f(x₁) ≠ f(x₂)

o, equivalentemente, se:

x₁,x₂ ∈ X | f(x₁) = f(x₂) ⇒ x₁ = x₂

ovvero x₁ e x₂ coincidono se l’immagine dei due elementi è la stessa.

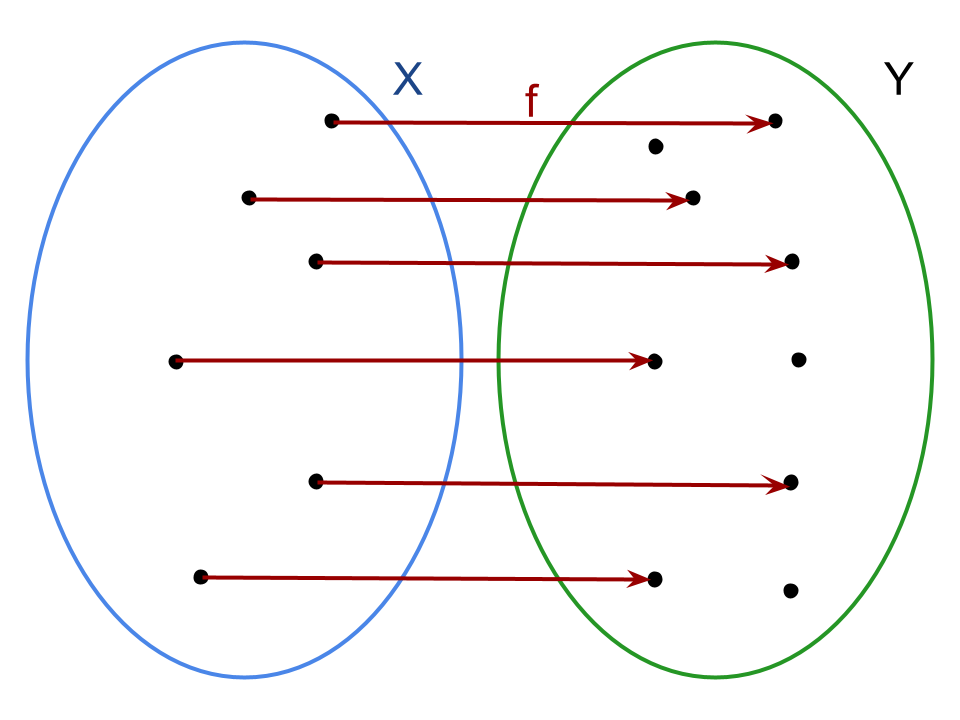
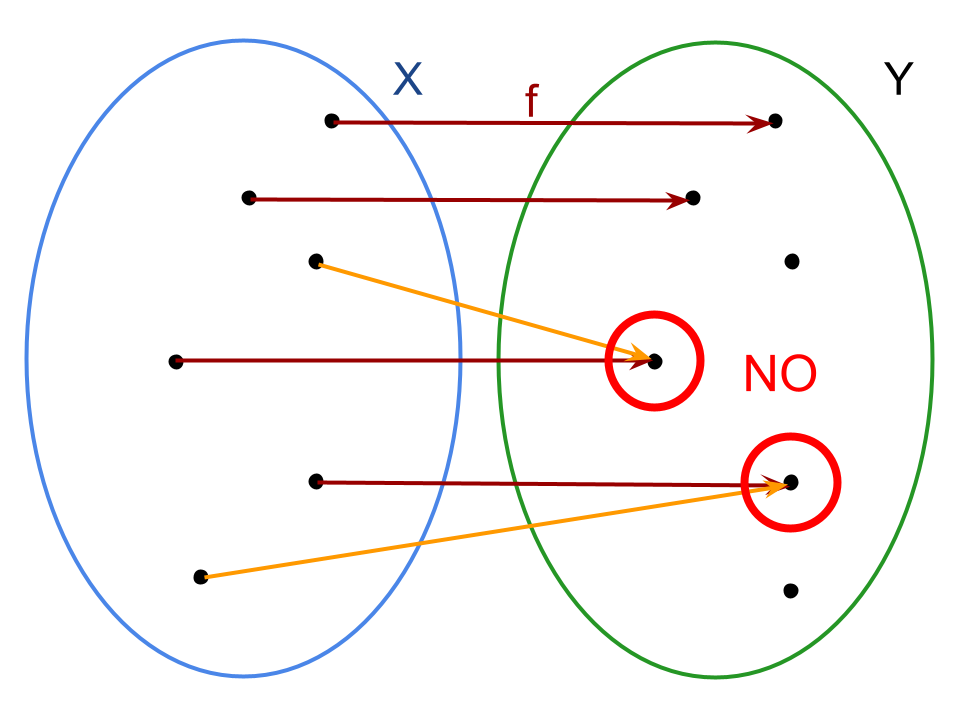
Come suggeriscono gli esempi grafici qui sopra, di fatto due elementi distinti appartenenti al dominio X non possono avere la stessa immagine in Y attraverso la legge f.

Nel caso più comune di funzioni reali di variabile reale esiste un metodo grafico per comprendere e verificare il concetto di iniettività: si traccino delle rette orizzontali y = k, con k ∈ ℝ, e si verifichi che tutte queste rette intersecano al massimo una volta il grafico della funzione.

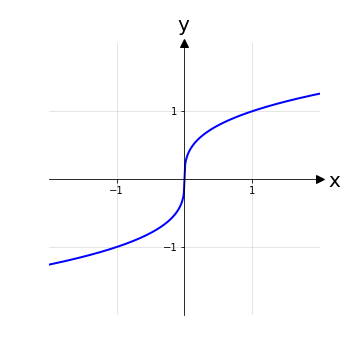
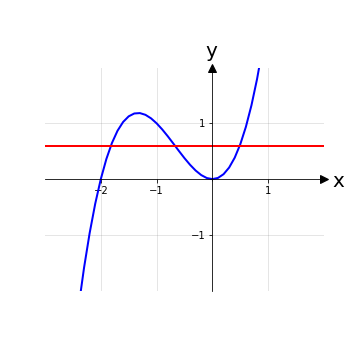
In generale, per dimostrare che una funzione non è iniettiva, basta:

• trovare due valori x₁ e x₂ appartenenti al dominio tali che f(x₁)=f(x₂)

• verificare che una retta orizzontale intersechi il grafico della funzione in più di due punti

Nota: Sia data una funzione f: X → Y dove il dominio sia un insieme con cardinalità, finita o infinita, superiore al codominio, allora f non può essere iniettiva.

Esempio 1: Siano dati A ≔ {a₁,a₂,a₃}, B ≔ {b₁,b₂} e si noti che card(A) = 3, card(B) =2. Dato che card(A) > card(B) è impossibile costruire una funzione iniettiva poiché è impossibile che uno dei due elementi di B non abbia 2 controimmagini.

Esempio 2: Un esempio più significativo si può fare considerando la funzione g: ℝ → ℕ, che in alcun modo può essere iniettiva: l’insieme ℝ dei numeri reali è un insieme con cardinalità infinita non numerabile, a differenza dell’insieme ℕ dei numeri naturali che è un’infinità numerabile.

Nota: Una funzione g: X → Y non iniettiva potrebbe diventarlo con una opportuna restrizione del dominio, in modo da escludere le y con più di una controimmagine.

Funzione suriettiva

Una funzione f: X → Y si dice suriettiva se ogni elemento di Y ha almeno una controimmagine in X; importante è notare la dicitura "almeno una controimmagine" che si traduce in una condizione che risulta soddisfatta anche se qualche elemento ha più di una controimmagine.

In linguaggio matematico, quindi, diremo che un’applicazione f: X → Y è suriettiva se è verificato che ∀y ∈ Y, ∃x ∈ X | f(x) = y o, equivalentemente, se ogni elemento di Y è immagine di almeno un elemento di X.

Nota: Se questa condizione è verificata insieme immagine im(X) e codominio Y ≔ cod(f) coincidono.

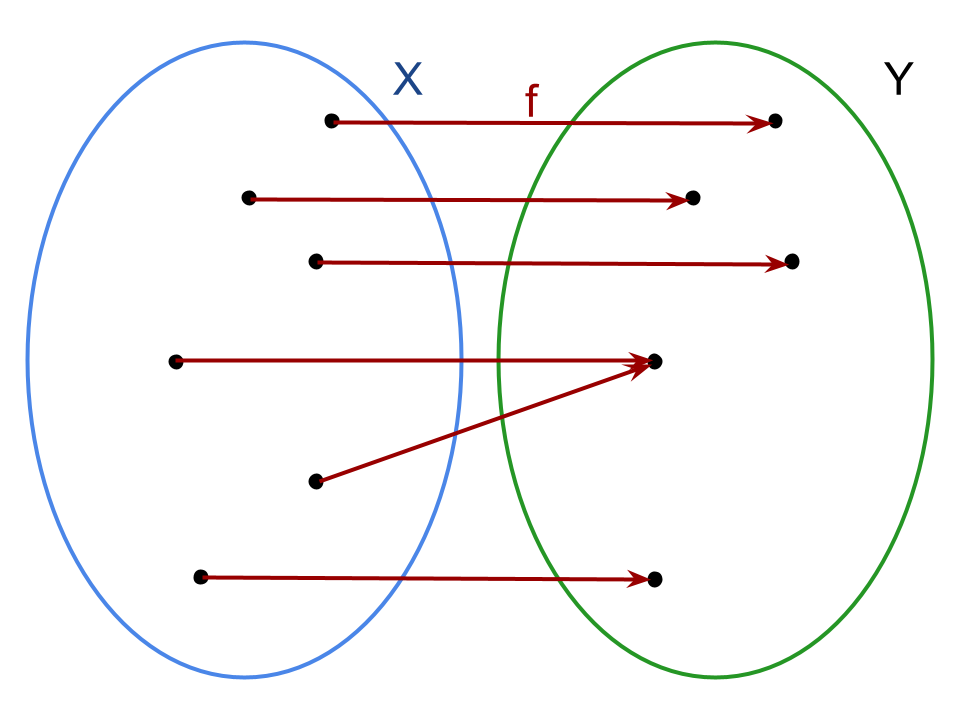
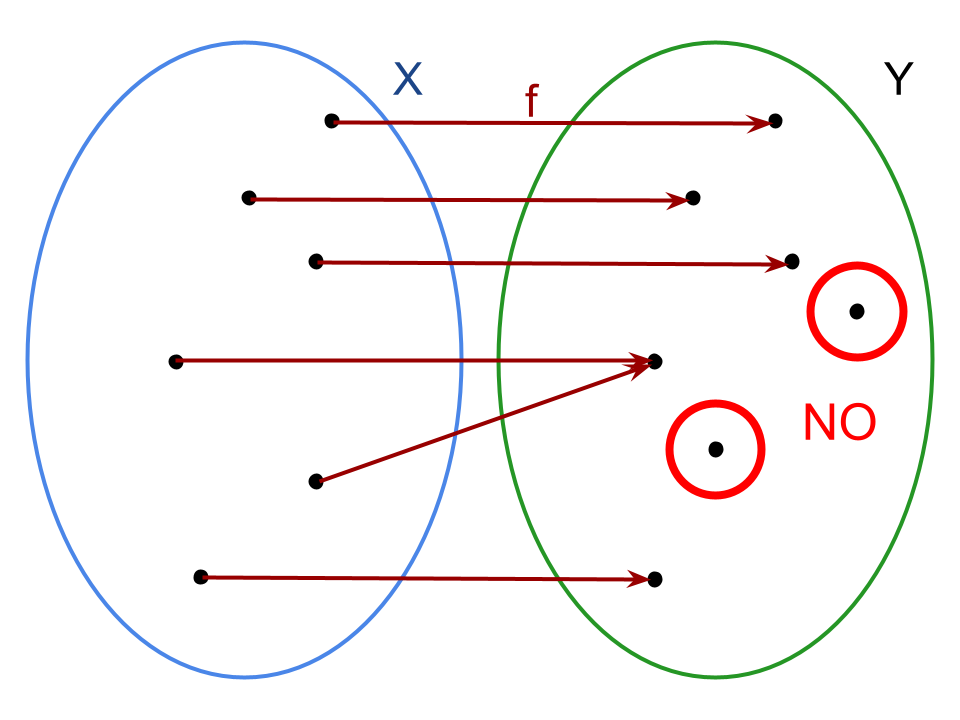
Come suggeriscono gli esempi grafici qui sopra, di fatto ogni elemento appartenente al codominio deve essere in relazione con almeno un elemento del dominio attraverso la legge f.

Nel caso più comune di funzioni reali di variabile reale esiste un metodo grafico per comprendere e verificare il concetto di suriettività: si traccino delle rette orizzontali y = k, con k ∈ ℝ, e si verifichi che tutte queste rette intersecano almeno una volta il grafico della funzione.

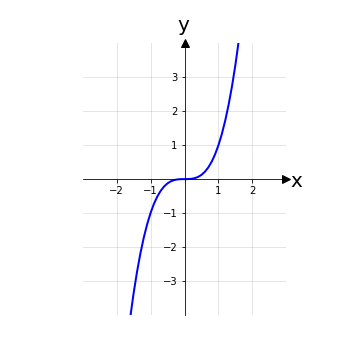
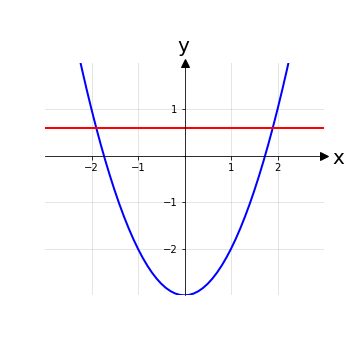
In generale, per dimostrare che una funzione non è suriettiva, basta:

• trovare un elemento del codominio che non ha controimmagine

• data la funzione f:X → Y, mostrare che im(X) ≠ cod(f) 

• verificare che una retta orizzontale non intersechi il grafico della funzione in almeno un punto

Esempio 3: La funzione "polinomiale" f: ℝ → ℝ definita dalla legge f(x) = 5x + 2 è suriettiva. Per verificarlo basta osservare che ∀y ∈ ℝ, ∃x ∈ X | y = f(x) = 5x + 2, dove l’elemento x che soddisfa la relazione è \(x = \frac{y-2}{5}\); per verifica si provi a sostituirlo nella legge f(x).   

Nota: Da una funzione g: X → Y non suriettiva si può ottenere una funzione g’ suriettiva definendola come g’: X → im(X), x ⟼ g(x), ovvero semplicemente definendo una funzione con stesso dominio e legge ma con un codominio "comodo".

Funzione biettiva

Una funzione f: X → Y si definisce biettiva o biunivoca se essa è sia iniettiva che suriettiva, o equivalentemente, se ogni elemento di Y ha una e una sola controimmagine in X. Una funzione biunivoca viene anche detta corrispondenza biunivoca o corrispondenza uno a uno, simbolicamente indicato con f: A ↔ B.

In linguaggio matematico, quindi, diremo che un’applicazione f: X → Y è biettiva se è verificato che ∀y ∈ Y, ∃! x ∈ X | f(x) = y o, equivalentemente, se ogni elemento di Y è immagine di un solo elemento di X. La definizione è molto simile a quella di suriettività, tuttavia è fondamentale notare la notazione "∃!" che indica che esiste un elemento ma è unico. Nel caso di funzioni suriettive invece l’unicità non è una condizione necessaria.

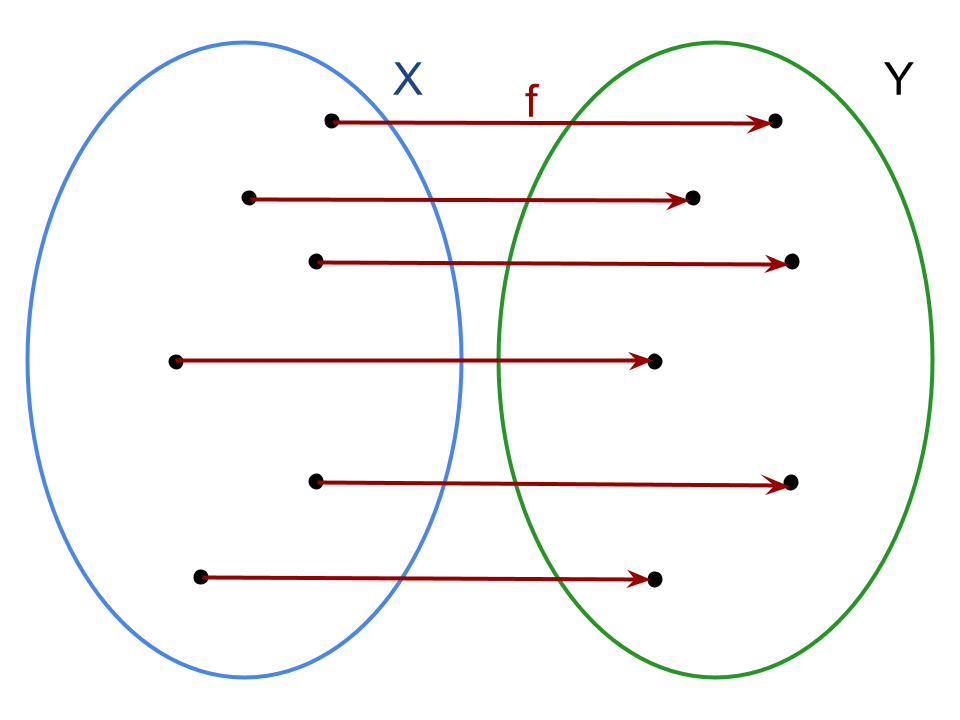
Come suggerito dall’esempio grafico sopra, di fatto ogni elemento del dominio deve essere in relazione uno a uno con un elemento del codominio attraverso la legge f.

Nel caso più comune di funzioni reali di variabile reale esiste un metodo grafico per comprendere e verificare il concetto di biettività ed è quello di tracciare delle rette orizzontali y = k, con k ∈ ℝ, e verificare che tutte queste rette intersecano sempre ed esattamente una volta il grafico della funzione.

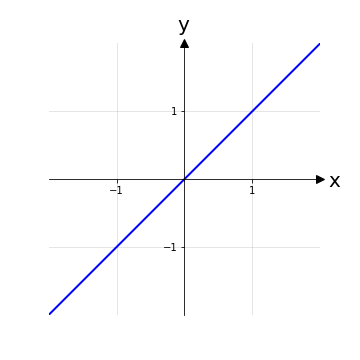
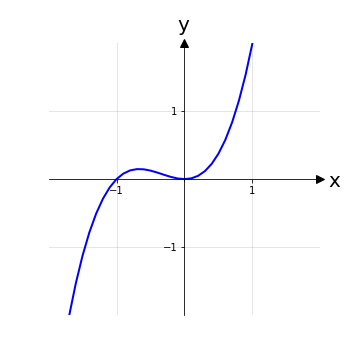
In generale, per dimostrare che una funzione non è biettiva, basta:

• dimostrare che non è suriettiva

• dimostrare che non è iniettiva

In particolare le proprietà di iniettività e suriettività, prese singolarmente, sono condizioni necessarie ma non sufficienti alla biettività: devono essere presenti entrambe.

Considerazioni finali

Osservazioni: 

• Le funzioni biettive f: X → Y sono invertibili: f-1: Y → X .

• Le funzioni iniettive g: X → Y sono invertibili con una opportuna restrizione del codominio affinché im(X) = cod(g), di fatto facendo guadagnare la suriettività alla funzione: g: X → im(X) .

• Le funzioni non iniettive possono diventarlo con opportune restrizioni del dominio.

Esempio 4: Una funzione periodica f: ℝ → ℝ, x ⟼ cos(x) non è né suriettiva né iniettiva come è facilmente verificabile con il metodo grafico. Altrimenti basta osservare banalmente che cos(x₁= 0) = 1 = cos(x₂= 𝜋) dove evidentemente x₁ ≠ x₂ e inoltre ∄x ∈ X | cos(x) = 2.

La funzione f può diventare biettiva con un’opportuna restrizione del dominio e del codominio, rispettivamente dom(f) ≔ [0, 𝜋) e cod(f) ≔ [-1,1].

Esempio 5: La funzione g: ℝ → ℝ | x ⟼ x è un esempio banale di funzione biettiva.

Nota: Le proprietà iniettiva e suriettiva trovano applicazione nella risoluzione di equazioni:

• la suriettività di una funzione indica che esiste almeno una soluzione (x₀) dell’equazione per ogni elemento del codominio

• l’iniettività  di una funzione segnala che, se la soluzione (x₀) dell’equazione esiste, essa è unica