Insieme immagine di una funzione

Data una funzione f: X → Y, x ⟼ f(x), sia X ≔ Dom(f). L’insieme immagine della funzione f, Im(f) o f(X), è definito come segue:

Im(f) ≔ { y ∈ Y | y = f(x) con x ∈ Dom(f) }  

In altre parole, l’insieme immagine della funzione f è la classe di tutti i punti f(x) ottenuti applicando al dominio la funzione f, ossia tutte le immagini di X attraverso la legge f. Una definizione simile, ma che non aggiunge nulla di nuovo, è la seguente:

Im(f) ≔ { ∀y ∈ Y, ∃ x ∈ X | y= f(x) }

Nota: Per definizione Im(f) ⊆ Cod(f), in particolare in questo caso Im(f) ⊆ Y. L’insieme immagine di una funzione è quindi un sottoinsieme del codominio della stessa funzione. Nel caso particolare in cui Im(f) = Cod(f) la funzione si dirà suriettiva e, banalmente, è possibile rendere una funzione suriettiva ridefinendo il codominio della funzione.

Passiamo ora a due metodi relativamente semplici per trovare l’insieme immagine di una funzione.

Metodo grafico

Una rappresentazione grafica di Im(f), nel caso di una funzione reale di variabile reale f: A ⊆ ℝ → ℝ, si riduce all’insieme delle ordinate nel piano cartesiano corrispondenti al Dom(A) attraverso f. 

Esempio 1: Sia data f: ℝ → ℝ, x ⟼ x² che rappresentiamo nel piano cartesiano:

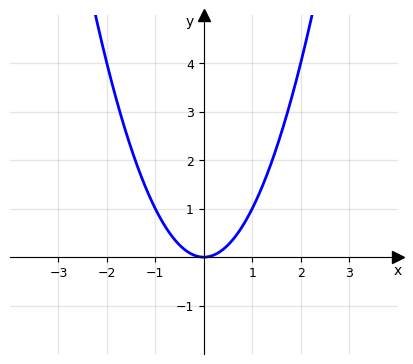
Dal grafico della funzione appare evidente come l’insieme immagine sia \(Im(f) = { y \in ℝ\; | \; y \ge 0 }\) poichè nessun punto del grafico della funzione ha ordinata minore di 0. In alternativa possiamo scrivere Im(f) ≔ [0.+∞), dove la parentesi quadra indica che il valore (0) appartiene all’insieme.

Esempio 2: Sia data g: ℝ → ℝ definita come 

\begin{equation} g(x) = \left\{\begin{array}{@{}l@{}l} x + 3 \quad quando \;\, x \geq 0\\ -x^2 \quad quando \;\, x < 0 \end{array}\right.\, \end{equation}

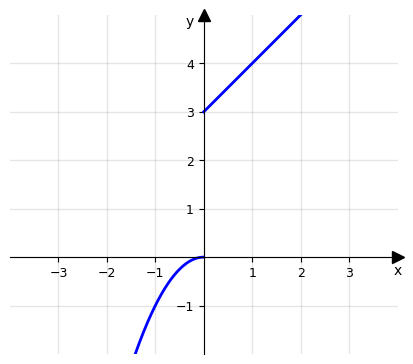
Dal grafico della funzione possiamo dedurre che Im(g) ≔ { y ∈ ℝ | y ≥ 3 ⋁ y < 0} = (-∞,0) U [3,+∞), dove la parentesi tonda indica che il valore 0 non appartiene all’insieme.

Esempio 3: Sia data h: ℝ⁺ → ℝ, x ⟼ ln(x) che rappresentiamo nel piano cartesiano:

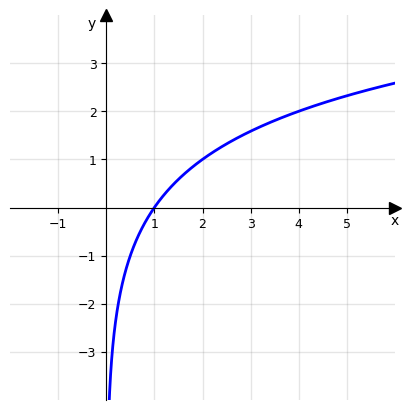
Dal grafico della funzione è evidente come Im(h) ≔ { y ∈ ℝ } = (-∞,+∞), poiché nell’avvicinarsi a 0 delle ascisse le f(x) tendono a diminuire sempre di più i propri valori (si dice che tendono a -∞). Allo stesso tempo, per valori di x crescenti, le f(x) continuano ad aumentare di valore (si dice che tendono a +∞).

Nota: Solitamente si utilizza questa notazione ℝ⁺ per indicare l’insieme ℝ⁺ ≔ {x ∈ ℝ | x > 0}.

Metodo analitico semplice

Seguono alcuni esempi che mostrano come, per trovare Im(f), nel caso di funzioni abbastanza semplici, sia sufficiente riuscire a esplicitare tutto in funzione della variabile indipendente x.  

Esempio 4: Sia dato X ≔ {1, 2, 3} e f: x ⟼ x2+3 e si voglia determinare l’insieme immagine della funzione f. In questo caso basta sostituire uno alla volta gli elementi del dominio nell’espressione di f e svolgere dei semplici passaggi algebrici.

\(f(1) = \sqrt{1^2+3} = \sqrt{4} = 2\)

Analogamente avremo:

\(f(2) = \sqrt{2^2+3} = \sqrt{7}\)

\(f(3) = \sqrt{3^2+3} = \sqrt{12}\)

Quindi l’insieme immagine di f, dato il dominio X, sarà \(f(X) ≔ {2, \sqrt{7}, \sqrt{12}\).

Esempio 5: Sia dato X ≔ ℝ e f: x ⟼ x+1.Per determinare l’insieme immagine Im(f) esplicitiamo la x in funzione della y.

y=x+1

x=y-1

che ha soluzione su tutto ℝ, che tra l’altro coincide con il codominio della funzione, ossia Im(f) ≔ {y ∈ Y} = cod(f). 

Esempio 6: Sia dato X ≔ ℝ e f: x ⟼ x2-4x-3.Per determinare l’insieme immagine Im(f) esplicitiamo la x in funzione della y.

\(y=x^2-4x-3\)

\(y+3=x^2-4x\)

completando il quadrato:

\(y+3+4= x^2-4x+4=(x-2)^2\)

\( \pm \sqrt{y+7}=x-2\)

\(x = 2 \pm \sqrt{y+7}\)

che ha soluzione solo per y+7≥ 0  ⇔  y≥ -7 ossia Im(f) ≔ {y ∈ Y | y ≥ -7} = [-7,+∞).

Esempio 7: Sia dato X ≔ ℝ e f: x ⟼ -1+x2+1. Per determinare l’insieme immagine Im(f) esplicitiamo la x in funzione della y.

\(y= -1+\sqrt{x^2+1}\)

\(y+1=\sqrt{x^2+1}\)

elevando al quadrato (radicando sempre ≥ 0 ∀x ∈ ℝ e imponendo y ≥ -1) :

\((y+1)^2=x^2+1\)

\(y^2+2y+1=x^2+1\)

\(y^2+2y=x^2\)

\(x= \pm \sqrt{y^2+2y}\)

che ha soluzione solo per y (y+2)≥ 0  ⇔  y≥ 0 ⋁ y≤ -2. Ma dato che prima abbiamo dovuto imporre y ≥ -1 possiamo tenere buono solo y ≥ 0, ossia Im(f) ≔ {y ∈ Y | y ≥ 0} = [0,+∞).
Nota: In generale, per trovare l’immagine di una funzione questo procedimento non sempre è applicabile e bisogna ricorrere ad un metodo analitico più raffinato che risulta molto simile allo studio di funzione. Per non appesantire troppa la trattazione non verrà riportato in questa pagina.