Grafico di una funzione inversa e legge analitica

Sia f una funzione invertibile, per determinare il grafico della sua inversa f^-1 possiamo notare che, preso un punto generico P(x,y) appartenente al grafico di f, vale la relazione f(x) = y. Dalla definizione di funzione inversa, abbiamo che f^-1(y) = x, ovvero se P(x,y) appartiene al grafico di f allora P’(y,x) appartiene al grafico di f^-1.

Inoltre un teorema ne garantisce l’unicità, ovvero, data una funzione invertibile, la sua funzione inversa è una e una soltanto.

Sia Gr(f) il simbolo con cui denotiamo il grafico della funzione f; matematicamente quanto detto sopra si tradurrà come:

se f invertibile allora P(x,y) ∈ Gr(f) ⇔ P’(y,x) ∈ Gr(f^-1)

Possiamo dunque notare come i grafici di f e f^-1 siano simmetrici rispetto alla bisettrice del primo e terzo quadrante del piano cartesiano. Di conseguenza per determinare il grafico dell’inversa di una funzione basta effettuare una simmetria rispetto alla retta di equazione y = x. In particolare:

• il segmento PP’ che congiunge i due punti (x,y) e (y,x) è perpendicolare alla bisettrice, cioè alla retta y = x

• la bisettrice interseca il segmento PP’ nel suo punto medio

Per determinare l’equazione di una funzione inversa basta esprimere, con passaggi algebrici, la x come funzione della variabile y, cioè x = f^-1(y).

Procedimento per il calcolo della funzione inversa

Sia data una generica funzione f: X → Y, x ⟼ f(x) dove f(x) è la legge con cui è definita. Se l’obiettivo è quello di trovare la legge della funzione inversa:

f^-1: f(X) → X, y ⟼ f^-1(y)

legge denotata da f^-1(x), occorre eseguire i seguenti passaggi:

1. Verifica dell’invertibilità di f:

   Come enunciato sopra, l’invertibilità delle funzione f è una condizione necessaria, e sufficiente, per poter avere una funzione inversa f^-1. Affinché una funzione sia invertibile è necessaria l’iniettività della stessa e il motivo è stato spiegato nella pagina "funzione invertibile".

   Per il metodo di verifica dell’iniettività di una funzione si rimanda agli esempi in “verifica dell’iniettività di una funzione”. Per ora si suppone soltanto che la funzione sia iniettiva o meno:

   • se la funzione è iniettiva ammette una funzione inversa e si procede a calcolarla con i passaggi successivi

   • se la funzione non è iniettiva si può cercare una restrizione del dominio che soddisfi l’iniettività, opzione approfondita nelle considerazioni finali in "funzioni iniettive, suriettive e biettive"

   • se la funzione non può essere resa iniettiva nemmeno con una restrizione del dominio allora non ha senso continuare nella ricerca della funzione inversa poiché non esiste

2. Individuare l’insieme immagine di f:

   La funzione inversa si è visto essere definita come f^-1: f(X) → X, y ⟼ f^-1(y) dove f(X) è l’insieme immagine della funzione f di partenza e bisogna verificare se esso coincide o meno con il codominio della funzione. In realtà che coincidano o meno non è veramente un problema, in quanto una opportuna restrizione del codominio è sempre applicabile senza modificare sostanzialmente la funzione [si veda la condizione di uguaglianza rilassata tra funzioni]; la cosa importante è stabilire quale sia il dominio della funzione inversa.

3. Calcolo algebrico della funzione inversa:

   Verificata l’iniettività e individuato il dominio f(X) dell’inversa si procede a calcolare la legge f^-1(y). Il procedimento non sempre è algebricamente facile, tuttavia concettualmente è semplice: basta riscrivere l’espressione 

   y = f(x)

   tramite passaggi algebrici e la conoscenza delle funzioni elementari, nella forma 

   x = f^-1(y)

   ossia esprimendo la x come funzione della nuova variabile indipendente y.

   Nota: Si ricordi che le variabili x e y sono mute, ossia non cambia concettualmente nulla scambiandole tra loro. Tuttavia, nel caso in cui si volesse graficare una funzione dalla legge f^-1 con una calcolatrice grafica, bisogna scambiare tra loro x e y, in pratica riscrivendo x = f^-1(y) nella forma y = f^-1(x). Questo potrebbe confondere ma quello che si sta facendo è semplicemente rinominare gli insiemi da

   f: X → Y, x ⟼ f(x)

   f^-1: f(X) → X, y ⟼ f^-1(y)

   a

   f: X → Y, x ⟼ f(x)

   f^-1: X → Y, x ⟼ f^-1(x)

   La scelta di mantenere X come dominio di f e f(X), sottoinsieme del codominio Y di f, come dominio di f^-1 è stata qua adottata solo per mantenere una certa coerenza e chiarezza nei passaggi.

Esempio

Determinare l’espressione analitica della funzione inversa delle seguenti funzioni:

1. f: ℝ → ℝ, x ⟼ f(x) con f(x) ≔ x²

2. g: ℝ\{-2} → ℝ, x ⟼ f(x) con \(g(x) ≔ \frac{2x-1}{x+2}+1\)

3. h: ℝ → ℝ⁺, x ⟼ f(x) con h(x) ≔ e^x+2 + 1

Riassumendo, la prima cosa da fare è verificare l’iniettività della funzione di partenza, poi trovarne l’insieme immagine e infine riscrivere y = f(x) nella forma x = f^-1(y).

1. La legge di f è quella che descrive una parabola quindi si può già intuire che non sia iniettiva. Per scrupolo lo verifichiamo scrivendo:

   x₁²  = x₂²

   e, facendo la radice quadrata ad entrambi i membri, otteniamo l’equazione

   ±x₁ = ±x₂  ⇒ x₁ = ±x₂

   dato che è ripetitivo il doppio ±.

   Dato che la funzione non è iniettiva ci si potrebbe fermare qua, tuttavia proviamo a titolo di esempio a trovare una sua restrizione che sia iniettiva: dato che questa funzione è simmetrica rispetto all’asse y, cioè f(x₁) = f(-x₁) ∀ x₁ ∈ ℝ, prendiamo solo metà del dominio, ad esempio ℝ⁺₀ . Visto che ci siamo notiamo che f(X) = ℝ⁺₀ e definiamo una nuova funzione f* simile alla precedente definita come

   f*: ℝ⁺₀ → ℝ⁺₀, x ⟼ f(x) con f(x) ≔ x²

   Questa funzione si può verificare essere iniettiva poiché, ripetendo gli stessi passaggi di prima, non si troverà una doppia soluzione (±) dato che abbiamo tolto gli elementi negativi.

   Si procede quindi con il calcolo della funzione inversa f*^-1(y) = x:

   y = x²

   \(y=\sqrt{x}\)

   La funzione così trovata è definita come f*^-1:  ℝ⁺₀ → ℝ⁺₀, y ⟼ f*^-1(y) con f*^-1(y) = y , che è sostanzialmente la funzione radice quadrata.

   

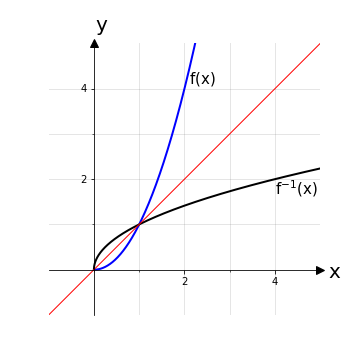
   Nota: Si tenga a mente che la funzione f*^-1 trovata non è l’inversa della funzione f di partenza, ma di una funzione con un dominio modificato f*.

2. La legge di g è del tipo polinomiale e, in generale, si può dedurre l’iniettività se non compaiono termini con potenza ad esponente pari. Il metodo di verifica è lo stesso usato in precedenza:

   \(\frac{2x_1-1}{x_1+2}+1 = \frac{2x_2-1}{x_2+2}+1\)

   \(\frac{2x_1-1}{x_1+2} = \frac{2x_2-1}{x_2+2}\)

   e, dato che abbiamo escluso -2 dal dominio, possiamo continuare con:

   (2x₁-1)(x₂+2) = (2x₂-1)(x₁+2)

   2x₁x₂ - x₂ + 4x₁ - 2 =  2x₂x₁ - x₁ + 4x₂ - 2

   5x₁ = 5x₂ ⇔ x₁ = x₂

   A priori, per quanto riguarda l’insieme immagine, è difficile capire se ci siano punti da escludere. Un modo di procedere è quello di raccogliere parte del numeratore in modo da semplificarlo con il denominatore. 

   \(y = \frac{2x-1}{x+2}+1\)

   \(y = \frac{2x-1-x+x+3-3}{x+2}+1\)

   \(y = \frac{(x+2)+(x-3)}{x+2}+1\)

   \(y = 1+\frac{x-3}{x+2}+1\)

   \(y = 2+\frac{(x+2)-3-2}{x+2}\)

   \(y = 3-\frac{5}{x+2}\)

   Da questa espressione si può dedurre che 3 è un valore che non può essere presente in Im(g) in quanto ∀x, \(\frac{5}{x+2}\) ≠ 0. In sintesi quindi g: ℝ\{-2} → ℝ\{3}.

   Procediamo con il calcolo della funzione inversa g^-1(y), facilitando i conti usando l’espressione equivalente trovata:

   \(y = 3-\frac{5}{x+2}\)

   \(x+2 = -\frac{5}{y - 3}\)

   \(x = -\frac{5}{y - 3} -2\)

   La funzione così trovata è ancora di tipo polinomiale ed è definita come g^-1: ℝ\{3}  → ℝ\{-2}, y ⟼ g^-1(y) con g^-1(y) \(= -\frac{5}{y - 3} -2\), equazione compatibile con i risultati precedentemente trovati su dominio e codominio di g.

   

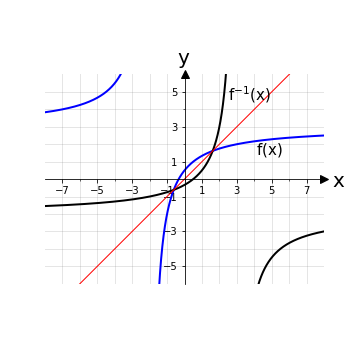
3. La legge di h è quella di un esponenziale "traslato" e se ne può verificare graficamente l’iniettività: nessuna retta parallela all’asse delle ascisse interseca più di una volta il grafico della funzione h. In alternativa si può verificare l’iniettività con il metodo usato per la funzione f: basta fare il logaritmo naturale (di base e) su entrambi i termini dell’equazione \(e^{x_1+2}=e^{x_2+2}\) , dopo un’opportuna semplificazione del termine costante +1 e una successiva semplificazione del termine costante +2.

   Verificato che la funzione è iniettiva su tutto il dominio ℝ, calcoliamo l’insieme immagine di h per capire quale sarà il dominio della sua inversa. In generale una funzione del tipo t(x) = e^x è definita come t: ℝ → ℝ⁺ e la traslazione orizzontale t(x) = e^x+2 non modifica la funzione, ma solo il punto in cui h(x) interseca l’asse delle ordinate. La traslazione verticale h(x) = e^x+2 +1 invece modifica l’insieme immagine che da ℝ⁺≔ {x ∈ ℝ | x > 0} diventa Im(h) ≔ {x ∈ ℝ | x > 1}.

   Procediamo con il calcolo della funzione inversa h^-1(y):

   y = e^x+2 + 1

   y - 1 = e^x+2

   ln (y - 1) = ln(e^x+2)

   assicurandoci che sia un’operazione lecita: la funzione logaritmo è del tipo t: ℝ⁺ → ℝ e, come abbiamo visto, Im(h) soddisfa questa condizione, cioè y - 1 > 0.

   ln (y - 1) = x + 2

   ln (y - 1) - 2 = x

   La funzione così trovata è definita come h^-1: Im(h) → ℝ, y ⟼ h^-1(y) con h^-1(y) = ln (y - 1) - 2, che è sostanzialmente una funzione logaritmica.

   

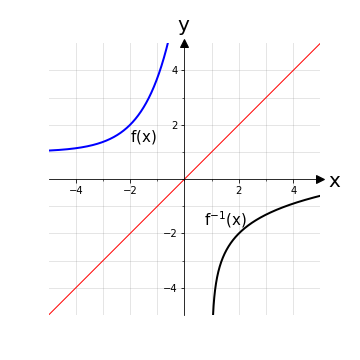
   Se si volesse verificare personalmente che il risultato sia giusto con una calcolatrice grafica si ricordi quanto detto nella Nota sopra sulle variabili mute (basta scambiare x con y).