Modulo e argomento di un numero complesso

Nella pagina "Numeri complessi e campo complesso" è stato introdotto il campo complesso descrivendone gli elementi, le operazioni e le proprietà mentre, nelle pagine "Piano di Gauss" e "Rappresentazione dei numeri complessi", sono state introdotte le varie rappresentazioni e, soprattutto, le coordinate polari.

In questa pagina ci si concentra su come calcolare modulo e argomento, quantità indotte dall’uso delle coordinate polari, di un numero complesso in qualsiasi rappresentazione.

Ricordando la definizione del campo complesso ℂ: 

ℂ ≔ {z ∈ ℂ | z = (x,y) con x,y ∈ ℝ}

cioè è l’insieme delle coppie ordinate (x,y) con x, y numeri reali. Come già visto, questa definizione si può ricondurre all’operazione di prodotto cartesiano tra insiemi: l’insieme dei numeri complessi è in corrispondenza biunivoca con il prodotto cartesiano ℝ x ℝ, anche denotato come ℝ². Per rappresentare i numeri complessi sfruttiamo quindi questa corrispondenza e utilizziamo il piano di Gauss per disegnare i grafici che serviranno.

Casi banali nella ricerca di modulo e argomento

Come nel piano cartesiano è possibile rappresentare univocamente qualsiasi punto usando le coordinate cartesiane o le coordinate polari, anche nel piano di Gauss è possibile fare la stessa cosa. Sia dato quindi un elemento z ∈ ℂ, z = (x,y).

Come esposto nella altre pagine, il numero complesso z può essere espresso in:

• forma cartesiana:

  z = x + iy

  dove x è detta parte reale di z, Re(z) ≔ x,  mentre y è detta parte immaginaria di z, Im(z) ≔ y.

  

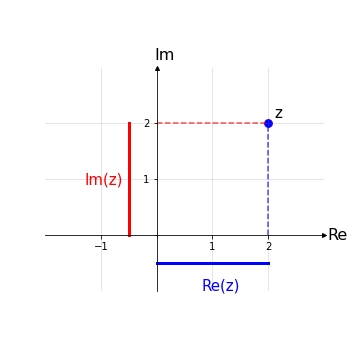
• forma trigonometrica:

  z = r (cosΦ+isinΦ)

  dove r è detto modulo di z, |z| ≔ r, e Φ è detto argomento di z, Arg(z).

  

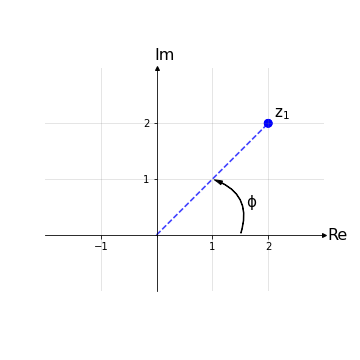
• forma esponenziale:

  \( z = re^{i\phi} \)

  dove le coordinate (r,Φ) sono sempre modulo e argomento, come nel caso della forma trigonometrica. 

Si può dedurre che, dato un numero complesso in forma esponenziale oppure trigonometrica, e quindi già in coordinate polari, per trovare modulo e argomento i passaggi siano banali.

Esempio 1: Sia dato il numero z = 5 cos(0) + i 5 sin(0)  e se ne trovino modulo |z| e argomento Arg(z).

Raccogliendo si trova:

z = 5(cos(0)+i sin(0))

e, confrontandolo con la rappresentazione trigonometrica, si trova banalmente che:

\(\left\{\begin{array}{@{}l@{}l} |z| = 5\\  \phi = 0 \end{array}\right.\,\)

Esempio 2: Sia dato il numero \( z = e^{i\left(\pi+\frac{\pi}{2}\right)} \)  e se ne trovino modulo |z| e argomento Arg(z).

Riscrivendo z come prodotto di un esponenziale per un numero reale e svolgendo l’operazione ad esponente si trova:

\( z = 1 e^{i\frac{3\pi}{2}} \)

e, confrontando il numero dato con la rappresentazione esponenziale, si trova banalmente che:

\(\left\{\begin{array}{@{}l@{}l} |z| = 1\\  \phi = \frac{3\pi}{2} \end{array}\right.\,\)

ll caso non banale è quanto il numero è dato in forma cartesiana o simil cartesiana del tipo

z₁ = 5 + i

z₂ = 2cos(0) + i sin(𝜋) 

In questo caso, per trovare |z_i| e Arg(z_i), bisogna studiare il legame che intercorre tra coordinate cartesiane e polari.

Modulo di un numero complesso

Sia dato un elemento z ∈ ℂ, z = (x,y) la cui rappresentazione cartesiana è z = x +iy.

Il modulo del numero complesso z, indicato con la notazione |z|, è un numero reale definito nel passaggio alle coordinate polari come:

\(|z| := \sqrt{x^2+y^2} =: r\)

Per definizione dell’operazione di radice si ha che |z| ≥ 0 ∀z e graficamente rappresenta il segmento che congiunge l’origine e il punto z nel piano di Gauss.

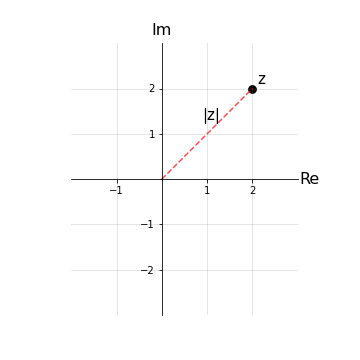
In particolare, il modulo ha le seguente proprietà:

• |z| = 0 ⇔ z = 0

• \(|z|^2 = z\overline{z} = x^2+y^2\) cioè \(|z| = \sqrt{z\overline{z}}\) e, inoltre, |z| ∈ [0,+∞).

Argomento o anomalia di un numero complesso

Sia dato lo stesso elemento z ∈ ℂ, z = (x,y) del paragrafo precedente.

L’argomento, o anomalia, del numero complesso z, indicato con la notazione Arg(z), è definito nel passaggio alle coordinate polari come:

\( Arg(z) := arctan(\frac{y}{x}) =: \phi\)

almeno nel primo quadrante (I q.) e graficamente rappresenta l’angolo, in senso antiorario, che il modulo |z| forma con l’asse positivo delle ascisse.

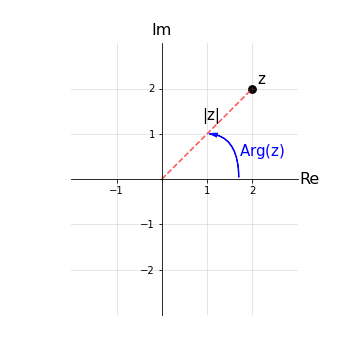
Tuttavia, se vogliamo rappresentare tutti i punti nel piano di Gauss, occorre che Arg(z) ∈ [0,2𝜋) oppure Arg(z) ∈ (-𝜋,𝜋] o un altro intervallo di ampiezza 2𝜋. La definizione dell’argomento diventa così dipendente dall’intervallo scelto e necessità ogni volta di considerare il quadrante in cui ci si trova.

Se scegliamo come intervallo Arg(z) ∈ [0,2𝜋) la sua definizione sarà la seguente:

\(\phi := \begin{cases} arctan(\frac{y}{x}) & \text{se $x>0$, $y\geq 0$ (I q.)} \\  arctan(\frac{y}{x})+2\pi & \text{se $x>0$, $y< 0$, (IV q.)}\\ arctan(\frac{y}{x})+\pi & \text{se $x<0$, $y< 0$, (II e III q.)}\\ \frac{\pi}{2} & \text{se $x=0$, $y>0$}\\  \frac{3\pi}{2} & \text{se $x=0$, $y<0$}\\  \text{non definito} & \text{se $x=0$, $y=0$} \end{cases}\)

Mentre se scegliamo come intervallo Arg(z) ∈ (-𝜋,𝜋] la sua definizione sarà leggermente modificata:

\(\phi := \begin{cases} arctan(\frac{y}{x}) & \text{se $x>0$, $y$ qualsiasi (I e IV q.)} \\  arctan(\frac{y}{x})+\pi & \text{se $x<0$, $y\geq0$, (II q.)}\\ arctan(\frac{y}{x})-\pi & \text{se $x<0$, $y<0$, (III q.)}\\ \frac{\pi}{2} & \text{se $x=0$, $y>0$}\\ \frac{3\pi}{2} & \text{se $x=0$, $y<0$}\\ \text{non definito} & \text{se $x=0$, $y=0$} \end{cases}\)

Nota: La necessità di individuare il quadrante in cui si è, discende, oltre a tenere conto dell’intervallo in cui Arg(z) è definito, discende dalle proprietà della funzione arcotangente. Per una prova empirica basti pensare che è valida la seguente uguaglianza:

\(arctan\left(\frac{y}{x}\right) = arctan\left(\frac{-y}{-x}\right)\)

cioè angoli del primo e del terzo quadrante restituiscono lo stesso valore per l’arcotangente.

Esempio 3: Sia dato il numero z = 2 + i2 e se ne trovino modulo |z| e argomento Arg(z).

Per il modulo applichiamo banalmente la definizione, individuando la parte reale Re(z) = 2 e la parte immaginaria Im(z) = 2. Per l’argomento invece poniamo innanzitutto come intervallo [0,2𝜋) e notiamo che Re(z), Im(z) > 0: z si trova nel primo quadrante e applichiamo la formula corrispondente.

\(\begin{cases} |z| = \sqrt{Re(z)^2+Im(z)^2} = \sqrt{8} \\  Arg(z) = arctan\left(\frac{Im(z)}{Re(z)}\right) = arctan(1) = \frac{\pi}{4} \end{cases}\)

Nota: Esempi più articolati sono esposti nella pagina "Coordinate cartesiane e polari per i numeri complessi".