Asintoti verticali: definizione ed esempi
Nell'universo dell'analisi matematica, gli asintoti verticali rappresentano una caratteristica intrigante e fondamentale di molte funzioni. Questi asintoti si manifestano come linee verticali verso le quali una funzione si avvicina infinitamente, senza mai toccarle, mentre l'input si avvicina a un valore particolare. Questa pagina esplora la natura, l'identificazione e l'importanza degli asintoti verticali, offrendo una guida approfondita per studenti e appassionati di matematica.
Che cosa sono gli asintoti verticali?
Un asintoto verticale è una retta verticale \(x=x_0\) a cui una funzione f(x) si avvicina infinitamente mentre x tende a \(x_0\), ma f(x) non assume mai il valore della retta. Gli asintoti verticali indicano, quindi, punti di discontinuità non superabili per la funzione, dove i valori di f(x) tendono a \(\pm\infty\).
Identificazione degli asintoti verticali
Gli asintoti verticali si manifestano in presenza di discontinuità nel dominio di una funzione, spesso dovute a divisioni per zero o a radici di numeri negativi in funzioni reali. Per identificare un asintoto verticale per \(x=x_0\), si cerca di determinare se il limite di f(x) tende a \(\pm\infty\) mentre x si avvicina a \(x_0\) da sinistra o da destra. Matematicamente, questo si esprime come:
\(\lim\limits_{x\to x_0^-}{f(x)}=\pm\infty\) oppure \(\lim\limits_{x\to x_0^+}{f(x)}=\pm\infty\)
Se uno di questi limiti è vero, allora \(x=x_0\) è un asintoto verticale di f(x).
In particolare, se il limite della funzione è infinito solamente per \(x\to x_0^-\), si parla di asintoto verticale sinitro, mentre se il limite della funzione è infinito solo per \(x\to x_0^+\), si parla di asintoto verticale destro.
Esempio di asintoto verticale
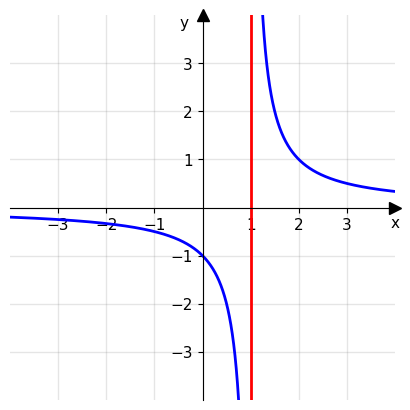
Un esempio classico di funzione con asintoto verticale è la funzione razionale \(f(x)=\frac{1}{x-1}\). In questo caso, x=1 è un asintoto verticale, poiché il limite di f(x) tende a \(\pm\infty\) mentre x si avvicina ad 1.
L'importanza degli asintoti verticali
Gli asintoti verticali sono fondamentali per comprendere il comportamento delle funzioni vicino ai punti di discontinuità e per analizzare la loro struttura. La presenza di asintoti verticali può influenzare l'integrabilità di una funzione, la convergenza di serie e integrali associati e la modellazione di fenomeni fisici e ingegneristici. La loro identificazione è cruciale nella graficazione delle funzioni, poiché segnalano comportamenti estremi e guidano la rappresentazione accurata delle funzioni nel piano cartesiano.
Gli asintoti verticali offrono una finestra sul comportamento infinito delle funzioni, servendo come sentinelle che segnalano punti di discontinuità insuperabile e crescita illimitata. La loro comprensione non solo arricchisce la nostra capacità di analizzare e rappresentare le funzioni matematiche ma apre anche la strada a un'applicazione più informata di questi concetti in contesti pratici.