Limite destro e limite sinistro di una funzione

Nell'ambito dell'analisi matematica, il concetto di limiti gioca un ruolo cruciale nella comprensione del comportamento delle funzioni in punti specifici o in prossimità di questi. Tra le varie tipologie di limiti, quelli destro e sinistro forniscono uno sguardo dettagliato sul comportamento di una funzione quando l'input si avvicina a un certo valore da una direzione specifica - da destra o da sinistra. Questa distinzione è fondamentale per studiare le funzioni che presentano discontinuità o punti di non definizione.

Il limite destro di una funzione f(x) in un punto \(x_0\) è il valore a cui f(x) si avvicina man mano che x si avvicina ad  \(x_0\) da valori maggiori di  \(x_0\). In termini matematici, questo limite è indicato come \(\lim_{x\to x_0^+} f(x)\), dove il simbolo + indica l'avvicinamento da destra.

Analogamente, il limite sinistro di una funzione f(x) in un punto \(x_0\) è il valore a cui f(x) si avvicina quando x si avvicina ad \(x_0\) da valori minori di \(x_0\). Questo è indicato come \(\lim_{x\to x_0^-} f(x)\), dove il simbolo - denota l'avvicinamento da sinistra.

Definizione matematica di limite destro e limite sinistro

Il limite destro di una funzione f(x) in un punto \(x_0\) si definisce come il valore che f(x) si avvicina quando x si avvicina ad \(x_0\) da valori maggiori di \(x_0\). Formalmente, si scrive:\(\lim_{x\to x_0^+} f(x)=L\)e si legge "il limite di f(x) per x che tende ad \(x_0\) da destra è L".

Questo significa che per ogni numero \(\epsilon>0\) (non importa quanto piccolo), esiste un numero \(\delta>0\) tale che se \(0<x-x_0<\delta\), allora \(\lvert f(x)-L\rvert < \epsilon\)

Mentre, il limite sinistro di una funzione f(x) in un punto \(x_0\) si definisce come il valore che f(x) si avvicina quando x si avvicina ad \(x_0\) da valori minori di \(x_0\). Formalmente, si scrive:\(\lim_{x\to x_0^-} f(x)=L\)

Analogamente al limite destro, ciò significa che per ogni \(\epsilon>0\), esiste un \(\delta>0\) tale che se \(0<x_0-x<\delta\), allora \(\lvert f(x)-L\rvert < \epsilon\)

Queste definizioni sono fondamentali nell'analisi del comportamento delle funzioni, specialmente vicino ai punti dove possono presentarsi discontinuità. La necessità di separare i concetti di limite destro e sinistro sorge dal fatto che una funzione può comportarsi in modo diverso quando ci si avvicina a un punto specifico \(x_0\) da direzioni diverse. Questa distinzione è essenziale per determinare la continuità di una funzione in un punto e per caratterizzare le discontinuità che possono verificarsi.

Esempio di limite destro e limite sinistro di una funzione

Consideriamo la funzione \(f(x)=\frac{1}{x}\) e calcoliamo il limite destro e sinistro quando x tende a 0:

• Limite destro: \(\lim_{x\to 0^+} \frac{1}{x}=+\infty\)
• Limite sinistro \(\lim_{x\to 0^-} \frac{1}{x}=-\infty\)

Questo comportamente è facilmente osservabile dal grafico della funzione:

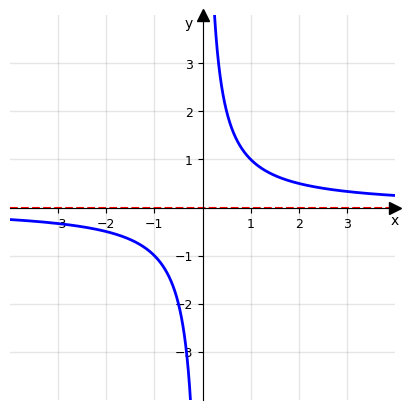
Questo esempio mostra chiaramente che i limiti destro e sinistro di una funzione possono differire tra di loro.

Importanza del limite destro e sinistro

La distinzione tra limite destro e sinistro è vitale in molteplici contesti:

1. Determinare la continuità: una funzione è continua in un punto \(x_0\) se e solo se il limite destro e il limite sinistro in quel punto sono uguali e corrispondono al valore della funzione in \(x_0\). Questa condizione fornisce una base per analizzare e classificare le discontinuità.
2. Analisi delle discontinuità: i limiti destro e sinistro aiutano a identificare e caratterizzare i tipi di discontinuità (come le discontinuità eliminabili, i salti e le discontinuità essenziali), fornendo una comprensione più profonda della struttura di una funzione.
3. Studio delle funzioni non definite in un punto: In molte situazioni, una funzione potrebbe non essere definita esattamente in \(x_0\) ma potrebbe comunque avvicinarsi a un valore specifico da una o entrambe le direzioni. I limiti destro e sinistro consentono di catturare questo comportamento.

I limiti destro e sinistro sono strumenti essenziali nell'analisi matematica, offrendo una visione dettagliata del comportamento delle funzioni vicino ai punti critici. La loro comprensione non solo arricchisce la nostra conoscenza teorica ma fornisce anche una base solida per applicazioni pratiche in vari campi della scienza e dell'ingegneria.