Limite finito per x che tende ad un valore infinito

Nell'ambito dell'analisi matematica, il concetto di limite gioca un ruolo cruciale nella comprensione del comportamento delle funzioni. Una categoria particolarmente interessante di limiti è quella dei limiti finiti per x che tende all'infinito. Questi limiti esplorano il comportamento delle funzioni mentre la variabile indipendente cresce senza limiti, sia in senso positivo (x→+∞) che negativo (x→−∞). La capacità di determinare il comportamento di una funzione a grandi distanze può offrire intuizioni significative in vari campi, dalla fisica all'ingegneria.

Un limite finito di una funzione f(x) mentre x tende all'infinito si verifica quando i valori di f(x) si avvicinano a un numero specifico L mentre x diventa arbitrariamente grande. Matematicamente, questo è espresso come:

• \(\lim_{x\to +\infty} f(x) = L\) indica che, man mano che x cresce senza limiti in senso positivo, i valori di f(x) si avvicinano a L.

• Analogamente, \(\lim_{x\to -\infty} f(x) = L\) indica che, man mano che x diventa arbitrariamente grande in senso negativo, i valori di f(x) tendono a L.

Definizione formale di limite per x che tende a infinito positivo

Si dice che \(\lim_{x\to +\infty} f(x) = L\) se, per ogni numero reale \(\epsilon >0\), esiste un numero reale M > 0 tale che se x > M, allora \(\lvert f(x)-L\rvert <\epsilon\). In altre parole, per x sufficientemente grande f(x) si trova entro una distanza arbitrariamente piccola da L.

Definizione formale di limite per x che tende a infinito negativo

Similmente, si dice che \(\lim_{x\to -\infty} f(x) = L\) se, per ogni numero reale \(\epsilon >0\), esiste un numeri reale N < 0 tale che se x < N, allora (\lvert f(x)-L\rvert <\epsilon\). Questo significa che per x sufficientemente piccolo (in valore negativo), f(x) si avvicina a L entro una distanza che possiamo rendere piccola a piacere.

Interpretazione delle definizioni formali

La definizione formale di un limite finito per x che tende all'infinito ci dice che non importa quanto lontano andiamo lungo l'asse delle x (positivamente per +∞ e negativamente per −∞), i valori della funzione f(x) si avvicineranno sempre più al valore L. Ciò che è cruciale qui è l'idea di "arbitrariamente vicino": possiamo rendere f(x) vicino a L quanto desideriamo semplicemente andando abbastanza lontano lungo l'asse delle x.

Esempi di limiti finiti per x che tende all’infinito

Prendiamo in considerazione alcune funzioni elementari per illustrare come si calcolano i limiti a infinito:

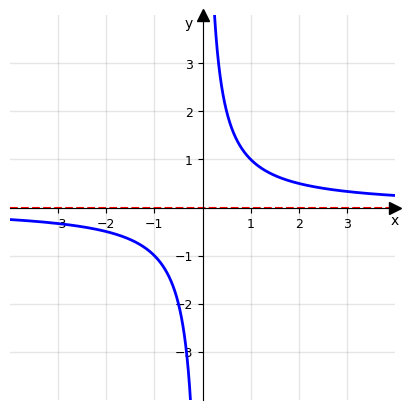
• Per la funzione \(f(x)=\frac{1}{x}\), vediamo che \(\lim_{x\to +\infty} \frac{1}{x} = 0\) e \(\lim_{x\to -\infty} \frac{1}{x} = 0\). Questo perché, man mano che x diventa molto grande (positivamente o negativamente), il valore di \(\frac{1}{x}\) diventa arbitrariamente piccolo, tendendo a zero.

  

• Ora, consideriamo la funzione \(f(x)=\frac{x}{x+1}\). In questo caso abbiamo che \(\lim_{x\to +\infty} \frac{x}{x+1} = 1\) e \(\lim_{x\to -\infty} \frac{x}{x+1} = 1\), questo comportamento è anche visibile nel grafico.

  

Importanza dei limiti che tendono all’infinito

I limiti a infinito sono fondamentali per diverse ragioni:

• Studio degli asintoti orizzontali: le funzioni con limiti finiti mentre tende all'infinito spesso hanno asintoti orizzontali. Queste sono linee orizzontali che la curva della funzione si avvicina man mano che x tende all'infinito, fornendo una visualizzazione grafica del limite.

• Analisi del comportamento a lungo termine: in molte applicazioni pratiche, capire come si comporta una funzione a grandi scale può aiutare a prevedere comportamenti futuri o a lungo termine di sistemi fisici, finanziari e altri sistemi modellati matematicamente.

• Ottimizzazione e crescita: nell'analisi economica, per esempio, conoscere il limite di una funzione di costo o profitto per grandi quantità può informare le decisioni strategiche su scala e crescita.