Partizioni e insieme quoziente

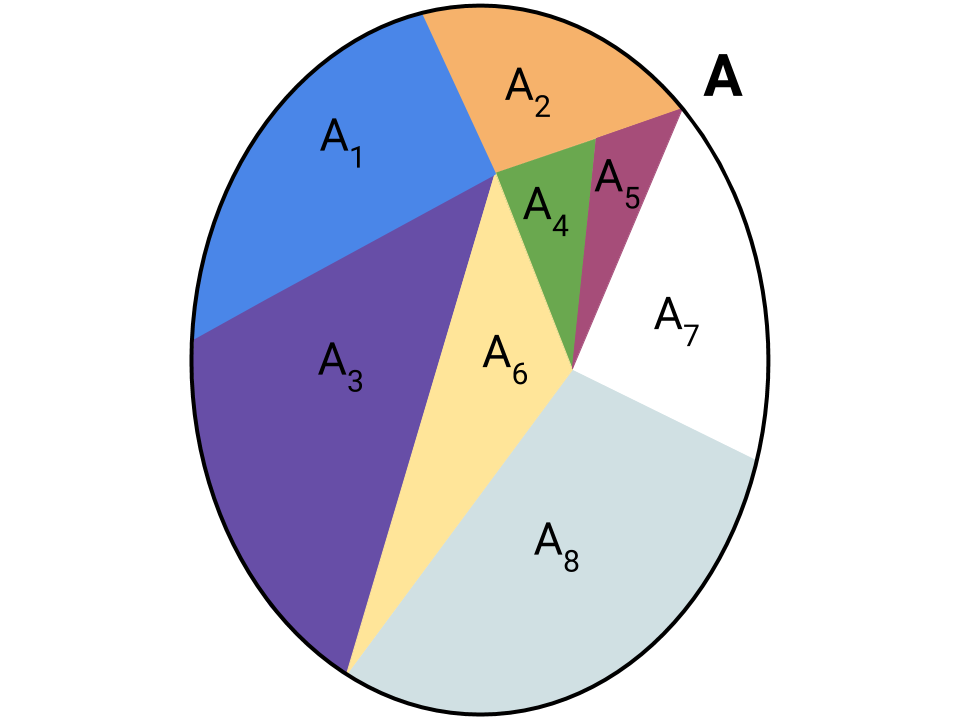
Dato un insieme X non vuoto definiamo una partizione 𝒮 di X una famiglia di sottoinsiemi di X stesso. Ricordando ℘(X) come l’insieme di tutti i sottoinsiemi propri e impropri di X [vedi insieme delle parti per maggiori dettagli] abbiamo quindi 𝒮 ⊆ ℘(X) tale che:

1. ∀ A ∈ 𝒮 si ha A ≠ {∅}, ovvero ogni insieme A ha almeno un elemento;

2. ∀ A₁, A₂ ∈ 𝒮 ⋀ A₁ ≠ A₂  ⇒ A₁ ∩ A₂ = ∅, ovvero due insieme appartenenti a 𝒮 non hanno elementi in comune a meno che non siano lo stesso insieme;

3. ⋃_{A ∈ 𝒮}  = X, ovvero l’unione di tutti gli insiemi A_i ∈ 𝒮 dà l’insieme X di partenza. 

Esempio 2: Dato X = ℕ si ha una sua partizione prendendo 𝒮 ≔ {P, D} con P l’insieme dei numeri pari e D l’insieme dei numeri dispari oppure 𝒮 ≔ {T, NT} con T l’insieme dei multipli di 3 e NT l’insieme dei numeri non multipli di 3 - sempre rimanendo nell’insieme dei naturali ℕ. 

Teorema: Dato in un insieme X non vuoto una relazione di equivalenza essa definisce una partizione nell’insieme in cui è definita. Tale partizione di X è costituita dall’insieme delle classi di equivalenza {[x] | x ∈ X} ed è detta insieme quoziente di X rispetto a ~. Si indica col simbolo X/~ .

Esempio 3: Riprendendo l’esempio 1, sia X l’insieme di tutte le automobili e ~ definita come “ha lo stesso colore di”. Allora tale relazione ~ definirà una partizione dell'insieme di partenza che può essere intuitivamente associato all’insieme di tutti i colori della automobili. 

Esempio 4: Si consideri la relazione di equivalenza definita come "modulo 2 con lo stesso risultato" nell'insieme ℕ. L’operazione di "modulo 2" consiste nel dividere il numero in questione per 2 e dà come risultato il resto della divisione; resto che intuitivamente può essere solo 0 o 1 in quanto un numero naturale può essere pari o dispari. Questa relazione, che si può verificare essere una equivalenza, dà origine ad esattamente due classi di equivalenza: [0] e [1] che contengono rispettivamente tutti i numeri pari e tutti i numeri dispari.

Dimostrazione: Basta dimostrare la validità delle 3 proprietà che definiscono una partizione:

1. [x] classe di equivalenza di x contiene almeno x ⇒ ∀ [x] ∈ {[x] | x ∈ X}, [x] ≠ ∅ ;

2. Per assurdo: Date [x] ≠ [y] due classi di equivalenza distinte supponiamo abbiano un elemento in comune k che falsifichi la proprietà; si ha quindi x ∿ k ⋀ y ∿ k ⇒ x ∿ y per la proprietà transitiva delle classi di equivalenza. Quindi essendo un altro qualsiasi elemento x’ ∈ [x], x’ ∿ x ⇒ x’ ∿ y e viceversa y’ ∈ [y], y’ ∿ y ⇒ y’ ∿ x ovvero [x] ⊆ [y] ⋀ [y] ⊆ [x] ⇒ [x] = [y] falsificando la tesi di partenza: due classi distinte non possono avere un elemento in comune ;

3. dato un qualsiasi x ∈ X si ha che x individua una classe [x] e quindi ∀ x ∈ X, ∃ [x] | x ∈ [x] e quindi {[x] | x ∈ X} = X.

Dalla dimostrazione della 2) discende che l’equivalenza, nel definire una partizione sull'insieme,  assegna univocamente ogni elemento ad un'unica classe di equivalenza [x]. In simboli ∀ x ∈ X, ∃! [x] | x ∈ [x].