Partizione e insieme delle parti

Prima di procedere suggeriamo di avere chiari i concetti di unione, intersezione, sottoinsieme e insieme vuoto. 

Insieme delle parti di un insieme

Dato un insieme X generico finito, l’insieme delle parti di X, indicato con la notazione ℘(X), è un insieme i cui elementi sono a loro volta insiemi, in particolare gli elementi corrispondono a tutti i possibili sottoinsiemi propri e impropri di X.

In particolare si può dimostrare che il numero di elementi di ℘(X) è pari a 2 elevato ad un numero che corrisponde alla cardinalità dell’insieme X su cui operiamo:

card(℘(X)) = 2^card(X)

Esempio 1: Sia dato A ≔ {10}. Determiniamo l’insieme delle parti ℘(A) scrivendo tutti i sottoinsiemi di B; in questo caso notiamo che si hanno solo due sottoinsiemi impropri che sono l’insieme vuoto ∅ e A stesso.

℘(A) ≔ { ∅, {1} } = { ∅, A }  

Notiamo che card(A) = 1 e che gli elementi di ℘(A) sono proprio 2^card(A) = 2.

Esempio 2: Sia dato B ≔ {0, 1, 2}. Determiniamo l’insieme delle parti ℘(B) scrivendo tutti i sottoinsiemi propri e impropri S_X di B:

Abbiamo quindi 8 insiemi che corrispondono agli elementi dell’insieme delle parti di B:

℘(B) ≔ { ∅, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0, 1, 2} }

Notiamo che card(B) = 3 e che gli elementi di ℘(B) sono proprio 2^card(B) = 8.

Nota: Si presti attenzione a non confondere l’elemento 0 con l’insieme vuoto ∅ e si ricordi che gli insiemi non hanno un ordine preferenziale: il sottoinsieme {1, 2} coincide con il sottoinsieme {2, 1}.

Partizione di un insieme

Dato un insieme X non vuoto definiamo una partizione 𝒮 di X una famiglia di sottoinsiemi di X stesso, A_k con k ≔ 1, 2, 3, …, n, che soddisfano le seguenti proprietà: 

1. ∀ A_k ∈ 𝒮 si ha A_k ≠ {∅}, ovvero ogni insieme A_k ha almeno un elemento;

2. ∀ A_k, A_j ∈ 𝒮 ⋀ k ≠ j  ⇒ A_k ∩ A_j = ∅, ovvero due insieme appartenenti a 𝒮 non hanno elementi in comune a meno che non siano lo stesso insieme (k = j);

3. ⋃_{A ∈ 𝒮}  = X, ovvero l’unione di tutti gli insiemi A_j ∈ 𝒮 dà l’insieme X di partenza. 

In particolare, ricordando l’insieme delle parti ℘(X) sopra definito, abbiamo che 𝒮 ⊆ ℘(X).

Utilizziamo un diagramma di Venn per rappresentare chiaramente il concetto di partizione di un insieme A in sottoinsiemi A_k tra loro disgiunti e che uniti restituiscono A:

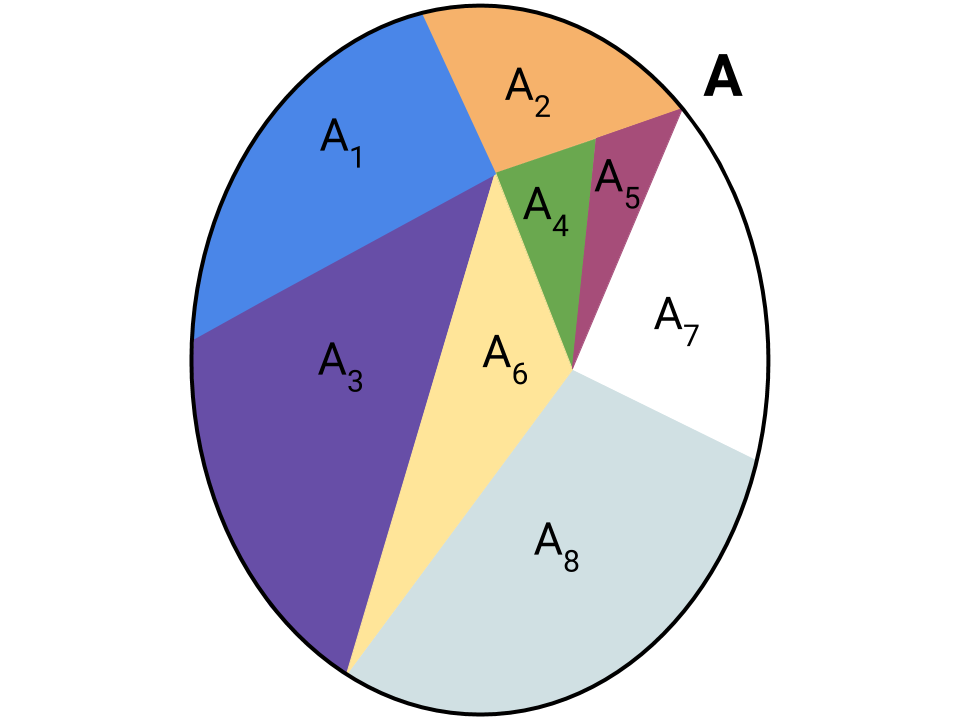
Esempio 1: Sia dato X ≔ {1, 2, 3, 4, 5} e gli insiemi A, B, C definiti come segue:

A ≔ {1, 2, 3}, B ≔ {3, 4}, C ≔ {5}. Ci chiediamo se A, B, C costituiscano o meno una partizione di X.

• osserviamo che A ≠ ∅, B ≠ ∅, C ≠ ∅ ;

• A ∩ B = {3}, A ∩ C = ∅, B ∩ C = ∅ ;

• A U B U C = {1, 2, 3, 4, 5} = X.

Tutte le condizioni sono verificate eccetto la 2, alla quale notiamo che gli insiemi A e B non sono disgiunti ma hanno un elemento in comune e quindi A, B e C non costituiscono una partizione di X. Si noti come, trovata la proprietà 2 falsificata, non sia necessario controllare la proprietà 3 per arrivare alla precedente conclusione.

Esempio 2: Sia dato X ≔ ℝ e siano dati gli insiemi A ≔ {x ∈ A | x < 0} e B ≔ {x ∈ B | x > 0} e si verifichi se A e B sono una partizione di X.

• osserviamo che A ≠ ∅ e B ≠ ∅;

• l’intersezione A ∩ B = ∅ ovvero non hanno elementi in comune;

• l’unione A U B = ℝ\{0} ovvero l’insieme dei reali ma privato dello zero.

Abbiamo quindi che A e B non costituiscono una partizione di X poiché la loro unione non restituisce completamente X. Per avere una partizione si può aggiungere un insieme C  ≔ {0} e così si ha 𝒮 ≔ {A, B, C}.
Esempio 3: dato X = ℕ si ha una sua partizione prendendo 𝒮 ≔ {P, D} con P l’insieme dei numeri pari e D l’insieme dei numeri dispari oppure 𝒮 ≔ {T, nT} con T l’insieme dei multipli di 3 e nT l’insieme dei numeri non multipli di 3 - sempre rimanendo nell’insieme dei naturali ℕ.