Intersezione tra insiemi

Avendo ben chiaro il concetto di insieme, sfruttando i diagrammi di Venn per visualizzare meglio le operazioni svolte e definendo un insieme universo U per evitare ambiguità, procediamo spiegando una delle principali operazioni insiemistiche.

Dati A, B due insieme generici contenuti in U, l’intersezione di A e B restituisce un nuovo insieme risultante A∩B che comprende tutti gli elementi che appartengono contemporaneamente ad entrambi gli insiemi dati. L’insieme risultante, intuitivamente contenuto anch’esso in U, è definito come:

A ∩ B ≔ {x ∈ U | x ∈ A ⋀ x ∈ B}

ovvero è l’insiemi costituito dagli elementi che appartengono simultaneamente ad entrambi gli insiemi di partenza. In particolare se A ∩ B = ∅ abbiamo due insiemi disgiunti, cioè che non hanno alcun oggetto in comune.

La rappresentazione con il diagramma di Venn dell’insieme intersezione corrisponde alla parte colorata in arancione nella seguente figura:

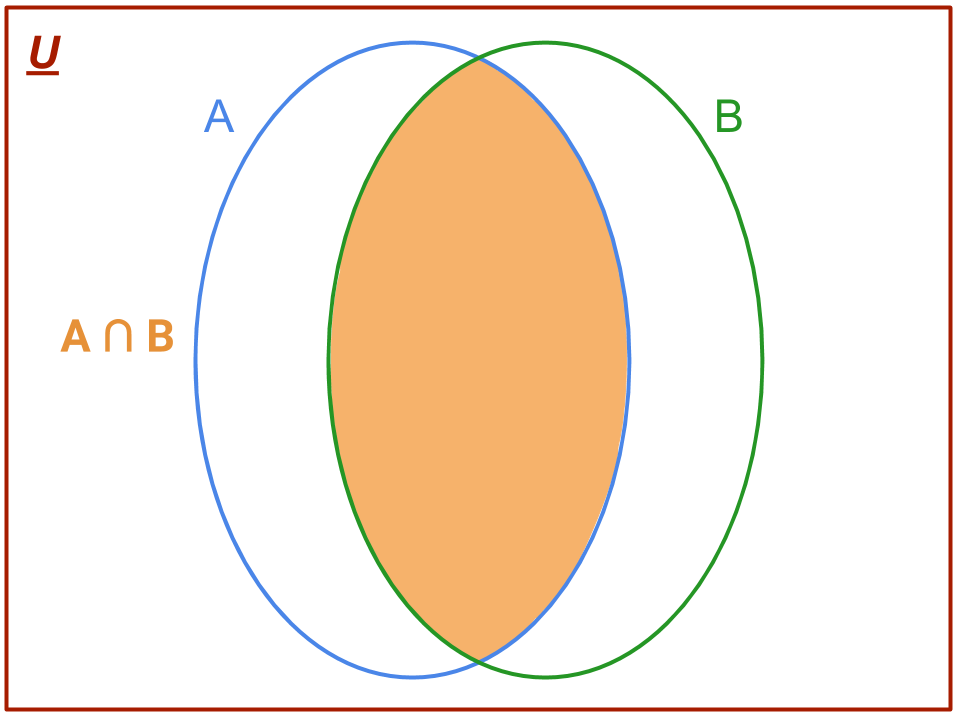
mentre per il caso particolare di insiemi disgiunti si ha:

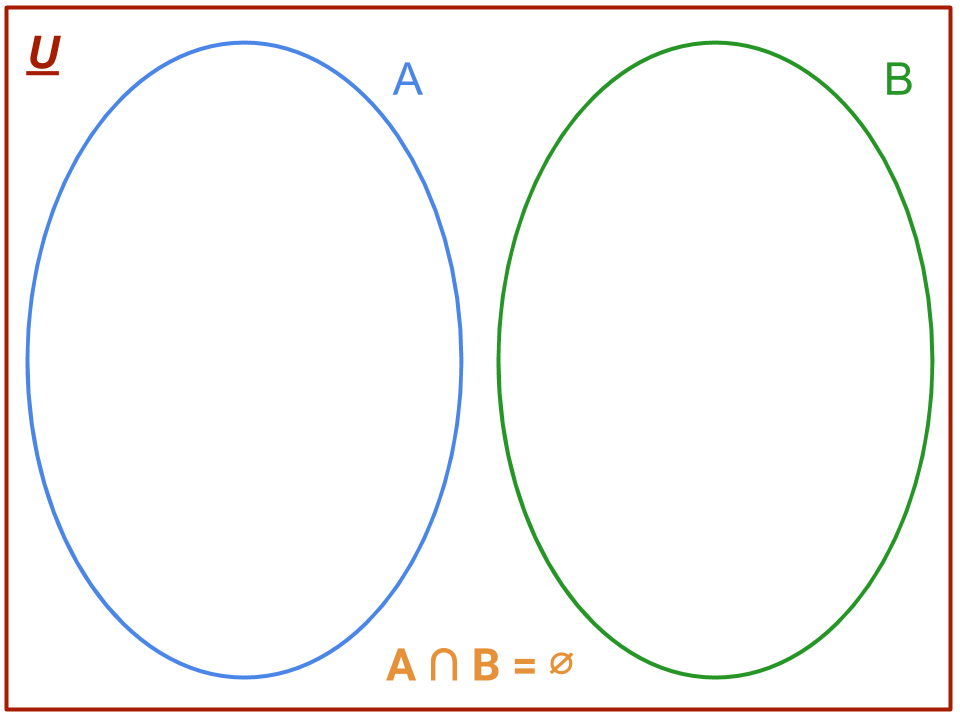
Esempio 1: Sia U ≔ ℕ e siano A, B, C alcuni suoi sottoinsiemi definiti come A ≔ {1, 2, 3, 4}, B ≔ {3, 4, 5}, C ≔ {5, 6, 7}. Intersecando i precedenti insiemi avremo:

A ∩ B = {3, 4}

A ∩ C  = ∅

B ∩ C = {5}

Si presti attenzione al fatto che gli elementi in comune non devono essere ripetuti: infatti, come visto nella definizione di insieme, è richiesto che tutti gli elementi siano distinti tra loro. La notazione A ∩ B = {3, 4, 3, 4} è da considerarsi un errore.

Esempio 2: Sia U ≔ ℕ e siano A, B due suoi sottoinsiemi definiti come A ≔ {x ∈ U | x ≥ 4}, B ≔ {x ∈ U | x ≥ 20}. Intersecando i precedenti insiemi avremo:

A ∩ B =  {x ∈ U | x ≥ 20} = B

in questo caso diremo che un insieme è contenuto nell’altro ovvero che B è sottoinsieme di A, B ⊂ A. 

Nota: ponendo U come ℚ o ℝ possiamo attuare l’operazione di intersezione anche tra insiemi densi e questo tornerà utile nell’Analisi Matematica.

Proprietà dell’intersezione tra insiemi

Posto un insieme universo U e dati tre suoi sottoinsiemi generici A, B, C, per l’operazione di intersezione valgono le seguenti proprietà:

1. l’intersezione di un qualsiasi insieme con sè stesso è equivalente all’insieme di partenza, infatti se B = A allora:

   A ∩ B = A ∩ A = A

   poiché vogliamo tutti gli elementi che appartengono ad entrambi gli insiemi simultaneamente;

2. l’intersezione di un qualsiasi insieme con ∅ è equivalente all’insieme vuoto ∅, posto B = ∅ allora:

   A ∩ B = A ∩ ∅ = ∅

   dato che vogliamo tutti gli elementi che appartengono ad entrambi gli insiemi, ma l’insieme vuoto ∅ per definizione non ha elementi;

3. l’intersezione di un qualsiasi insieme con un suo sottoinsieme coincide con il sottoinsieme stesso, infatti posto per ipotesi A ⊆ B si ha che:

   A ∩ B = A

   visto che per definizione di sottoinsieme tutti gli elementi di A appartengono a B;

4. l’intersezione di un qualsiasi insieme con l’insieme ambiente U coincide l’insieme stesso:

   A ∩ U = A

   e la spiegazione è analoga alla proprietà 3 dato che per ipotesi A ⊆ U;

5. l’intersezione di un qualsiasi insieme con la sua unione con un secondo insieme è uguale al primo insieme di partenza:

   A ∩ (A U B) = A

   per il semplice fatto che possiamo applicare la proprietà 3 dato che A ⊆ A U B;

Nota: le precedenti 5 proprietà sono tutte casistiche particolari della proprietà di inclusione n.3. In particolare si ricordi la nozione di sottoinsiemi impropri per la quale ∅, A ⊆ A.

• l’intersezione tra due insiemi è commutativa:

  A ∩ B = B ∩ A

  poiché nella nozione di insieme non ha importanza l’ordine con cui vengono presi gli elementi;

• l’intersezione tra due insiemi è associativa:

  (A ∩ B) ∩ C = A ∩ (B ∩ C)

  sempre per il fatto che l’ordine dei termini non ha importanza;

• l’intersezione tra due insiemi è distributiva rispetto all’unione:

  A ∩ (B U C) = (A ∩ B) U (A ∩ C)

  e ciò è facilmente verificabile con dei diagrammi di Venn;

• il complementare dell’intersezione corrisponde all’unione dei complementari dei singoli insiemi (Legge di De Morgan):

  𝓒 (A ∩ B) = 𝓒 A U 𝓒 B

  e ciò è facilmente verificabile con dei diagrammi di Venn come mostrato nell’apposita lezione;

• l’intersezione di un insieme con il suo complementare coincide con l’insieme vuoto ∅:

  A ∩ 𝓒 A = ∅

  per definizione di complementare oltre che a essere verificabile con dei diagrammi di Venn.

Riassumiamo le 10 proprietà nella seguente tabella seguendo l’ordine precedente.