Sottoinsiemi propri e impropri

Definito un insieme come una raccolta di elementi, un sottoinsieme non è altro che un insieme che contiene parte degli elementi di un altro insieme più grande. Dato un insieme A generico, l’insieme B che contiene parte dei suoi elementi si dirà suo sottoinsieme e si indicherà con la notazione B ⊆ A, ovvero l’insieme B è contenuto in A.

Per dare una definizione rigorosa si dice che B è sottoinsieme di A se e solo se ogni elemento di B appartiene anche a A, ovvero:

B ⊆ A ⇔ ∀ x | x ∈ B, x ∈ A

Nota: importante è il quantificatore logico ∀ perché se l’insieme B dovesse contenere anche un solo elemento che non appartiene all’insieme A, B non potrebbe essere più definito come sottoinsieme di A.

Nella rappresentazione grafico con il diagramma di Venn un sottoinsieme appare come una figura dal perimetro chiuso e non intrecciato contenuta totalmente in una figura più grande che sarà l’insieme di partenza come segue:

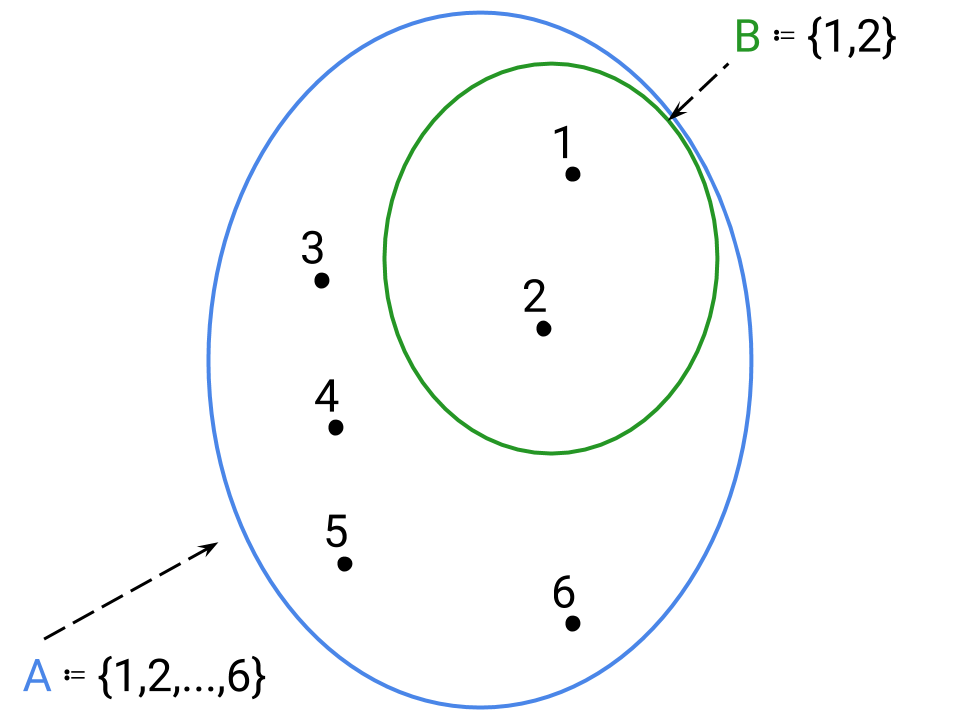
dove chiaramente B ⊆ A dato che possiede i soli elementi 1 e 2 che appartengono anche ad A.

Sottoinsiemi propri e impropri

I sottoinsiemi si suddividono poi in due categorie: i sottoinsiemi propri e i sottoinsiemi impropri.

• Sottoinsiemi propri: Dato un insiemi A generico e B un suo sottoinsieme, B si dirà sottoinsieme proprio di A se esiste almeno un elemento di A che non appartiene a B:

  B ⊂ A ⇔ ∀ x | x ∈ B, x ∈ A  ⋀  ∃ x ∈ A | x ∉ B

  dove nel membro di destra la condizione b ∈ A indica che B deve essere ovviamente sottoinsieme, altrimenti non ci si pone nemmeno la domanda se sia proprio o meno.  

Esempio 1: Sia A ≔ {x | x ∈ ℕ ⋀ x ≤ 10 ⋀ x ≠ 0} e siano B, C, D suoi sottoinsiemi propri definiti come B ≔ {1}, C ≔ {2, 3, 4, 5, 6}, D ≔ {6, 7, 8, 9, 10}.

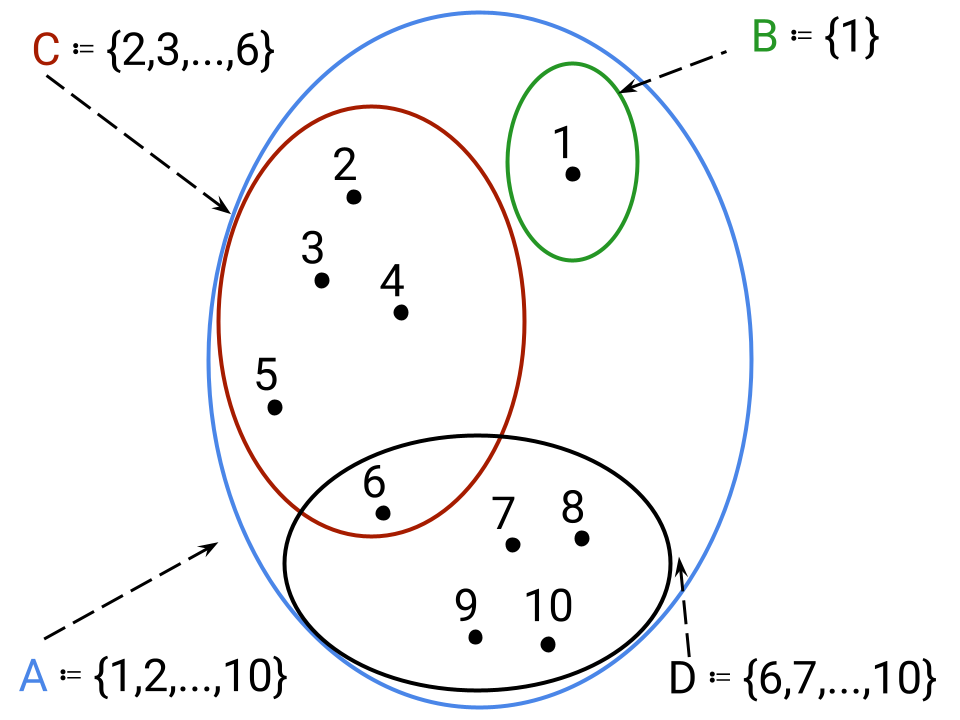
Come si può dedurre B, C e D non sono gli unici sottoinsiemi propri di A ma per approfondire rimandiamo al concetto di insieme delle parti. 

Esempio 2: Sia A ≔ ℚ insieme dei numeri razionali e B ≔ ℕ insieme dei numeri naturali. Banalmente B ⊂ di A e si grafica, ricordando la rappresentazione per insiemi infiniti, come segue   

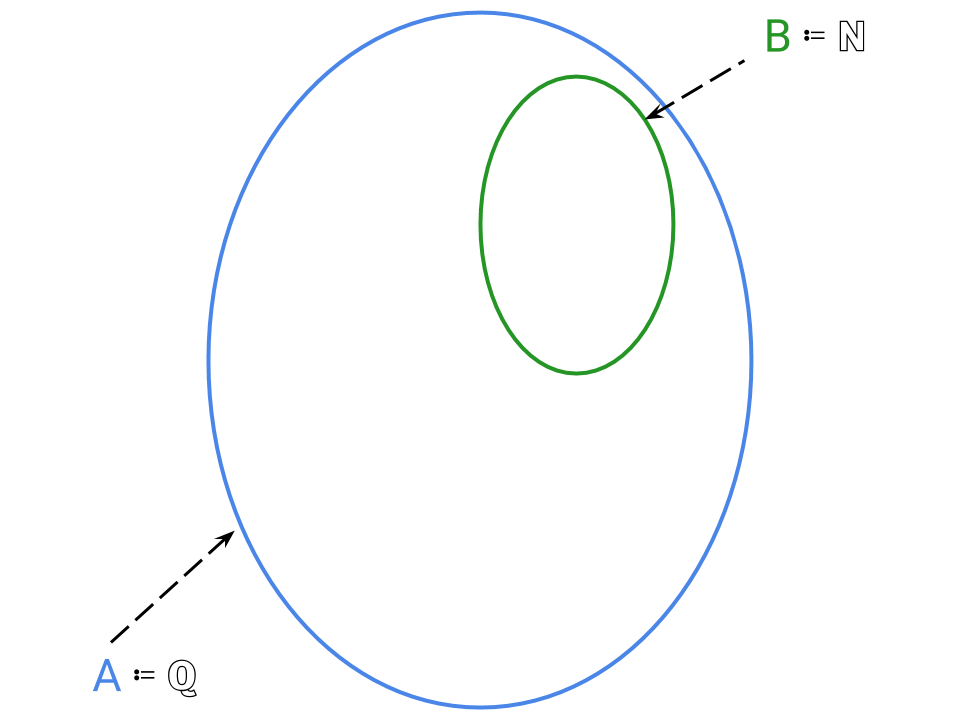
• Sottoinsiemi impropri: Dato un insiemi A generico e B un suo sottoinsieme, B si dirà sottoinsieme improprio di A se B è l’insieme vuoto ∅ oppure se B coincide con A stesso:

  B = ∅  ⋁  B = A

  In particolare se B = A si userà la seguente notazione B ⊆ A. Si noti che i sottoinsiemi impropri sono sempre e solo due.

Nota: è bene prestare attenzione alla differenza tra i simboli ⊂ e ⊆. Infatti il primo indica una inclusione stretta mentre il secondo descrive una inclusione meno rigida che ammette anche l’uguaglianza tra i due insiemi; il concetto è analogo ai simboli <, ≤ e >, ≥.