Insieme vuoto: definizione, proprietà ed esempi

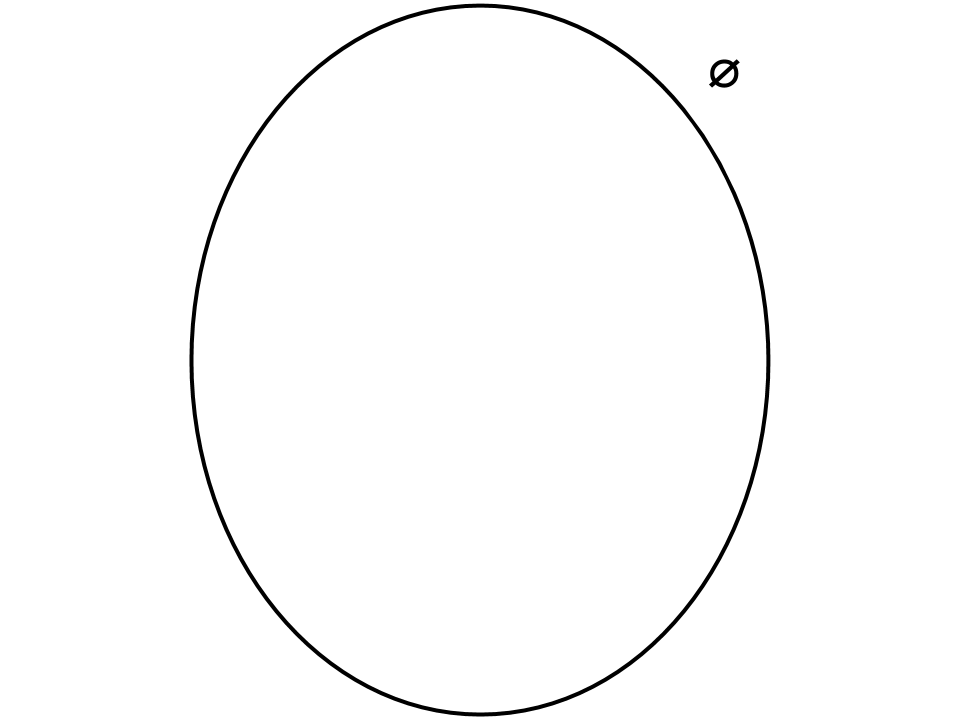
Definito un insieme come una raccolta di elementi, si ammette un insieme particolare che non contiene alcun elemento: l’insieme vuoto, indicato con il simbolo ∅ o con le parentesi graffe vuote { }. La sua rappresentazione con il diagramma di Venn prevede una linea chiusa non intrecciata che però non contiene punti/elementi.

Esempio 1: Sia A ≔ {l’insieme dei numeri naturali strettamente minori di 0}. Per definizione, ℕ non ammette numeri negativi, per cui l’insieme A non contiene alcun elemento: A = ∅.

Esempio 2: Sia B ≔ {x ∈ ℕ | x + 1 = 0} e questo insieme, che prende numeri dall’insieme dei naturali ℕ, risulta essere vuoto: B = ∅.  

Esempio 3: Sia C ≔ {x ∈ ℝ | x² = -1} e questo insieme, che prende numeri dall’insieme dei reali ℝ, risulta essere vuoto: C = ∅. Questo esempio è simile al precedente e affinchè gli insiemi B e C non siano vuoti occorre cambiare insieme numerico.

Dai precedenti esempi A, B e C sono insiemi sostanzialmente equivalenti, pur avendo diverse definizioni. Dalla definizione di uguaglianza tra insiemi due insiemi sono uguali se ogni elemento del primo appartiene anche al secondo e viceversa ma, in questo caso, gli insiemi non contengono elementi e quindi la condizione non può essere falsificata. Ne deriva che esiste un unico insieme vuoto ∅.

Nota: Il diagramma di Venn dell’insieme vuoto potrebbe creare confusione poiché la rappresentazione per un insieme con infiniti elementi è analoga: come discriminante tra i due casi poniamo per convenzione che il nome dell’insieme, se vuoto, sarà appunto ∅.

Le proprietà dell'insieme vuoto

Riportiamo nella seguente tabella le proprietà più comuni dell’insieme vuoto ∅. Sia dato un insieme A generico, anche vuoto:

Con U nell’ultima proprietà ci si riferisce all’insieme universo considerato.