Leggi di De Morgan: definizione, spiegazione ed esempi
Le leggi di De Morgan sono delle regole di operazione tra gli insiemi che mettono in relazione le operazione insiemistiche di unione, intersezione e complementazione permettendo di semplificare i passaggi.
Prima legge di De Morgan
Dato un insieme universo U e due suoi sottoinsiemi generici A, B, la prima legge di De Morgan afferma che il complementare dell’intersezione di due insiemi è uguale all’unione dei complementari dei rispettivi insiemi, ovvero:
𝓒 (A ∩ B) = 𝓒 A U 𝓒 B
Dimostrazione: per chiarezza e semplicità utilizziamo i diagrammi di Venn ma è possibile verificare la veridicità dell’uguaglianza sopra anche applicando le definizioni di insieme unione, intersezione e complementare.
Procediamo graficando il primo membro dell’uguaglianza, 𝓒 (A ∩ B), che coloriamo in arancione nel seguente diagramma di Venn:
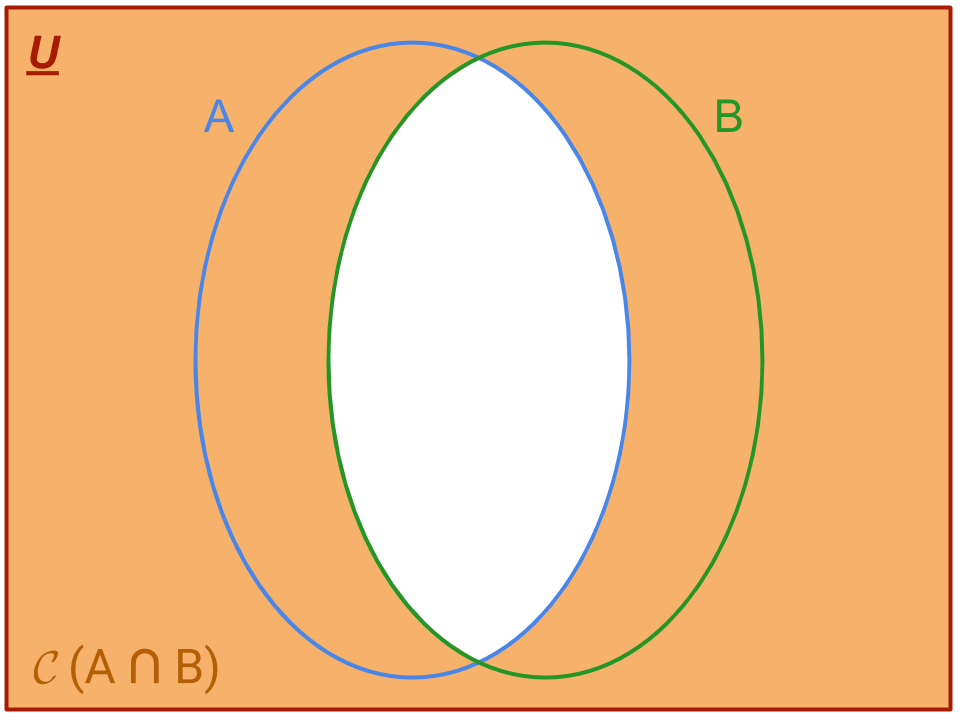
che otteniamo individuando l’insieme A ∩ B ed evidenziando tutto ciò che è contenuto in U che non appartiene a tale insieme, secondo la definizione di complementare.
Ora non resta che graficare il secondo membro dell’uguaglianza, 𝓒 A U 𝓒 B, e verificare che i due diagrammi coincidano. Procediamo graficando gli insiemi 𝓒 A e 𝓒 B rispettivamente:
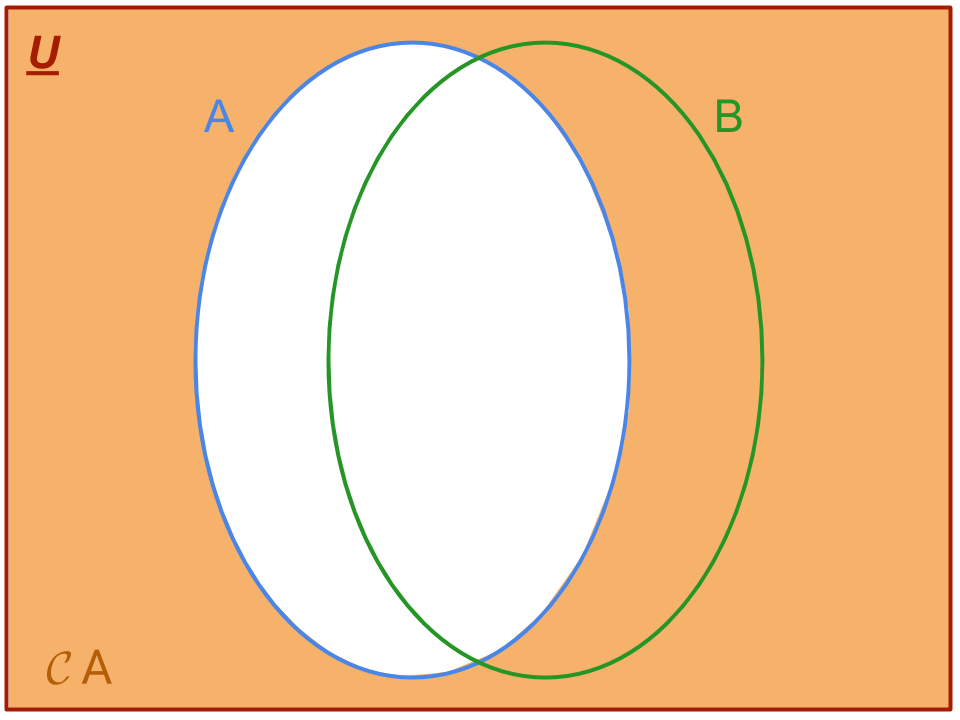
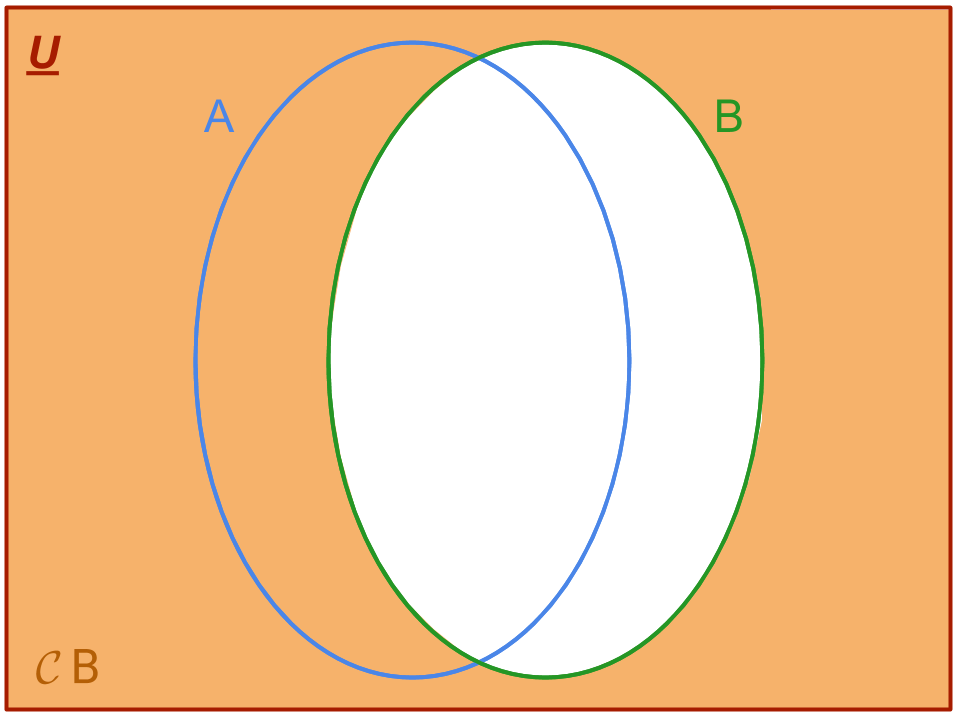
e operando l’unione si ha l’insieme finale, il cui diagramma di Venn osserviamo essere uguale a quello dell’insieme 𝓒 (A ∩ B):

poichè l’intersezione A ∩ B è l’unico insieme a non essere colorato. Questa dimostrazione è così conclusa.
Seconda legge di De Morgan
Dato un insieme universo U e due suoi sottoinsiemi generici A, B, la seconda legge di De Morgan afferma che il complementare dell’unione di due insiemi è uguale all’intersezione dei complementari dei rispettivi insiemi, ovvero:
𝓒 (A U B) = 𝓒 A ∩ 𝓒 B
Dimostrazione: come prima utilizziamo i diagrammi di Venn ricordando che è non l’unico metodo percorribile.
Procediamo graficando il primo membro dell’uguaglianza, 𝓒 (A U B), che coloriamo in arancione nel seguente diagramma di Venn:
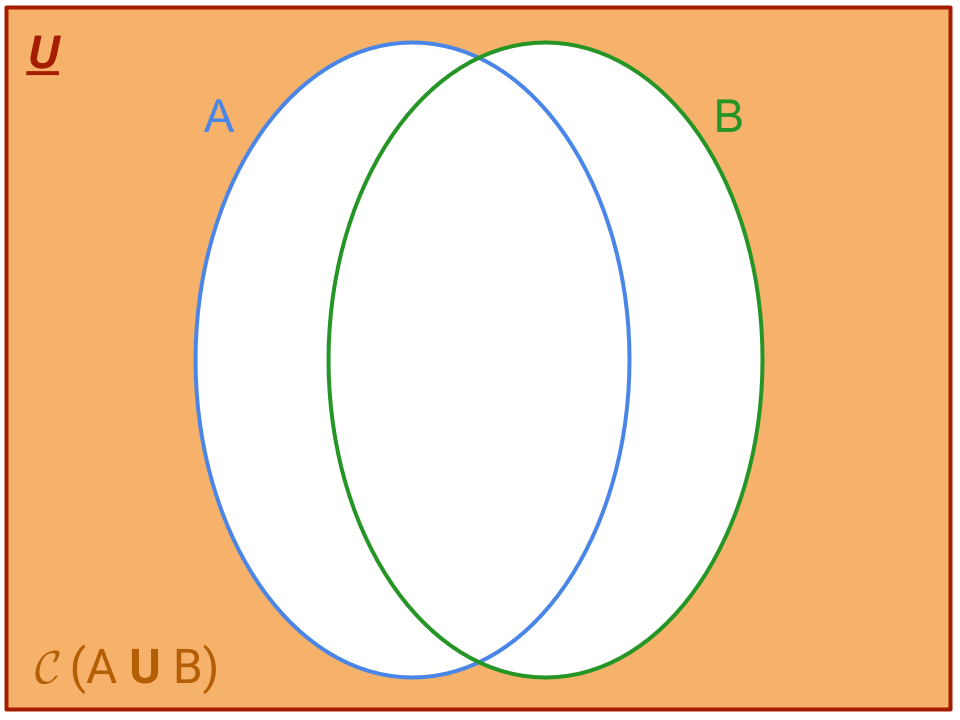
che otteniamo individuando l’insieme A U B ed evidenziando tutto ciò che è contenuto in U che non appartiene a tale insieme, sempre secondo la definizione di complementare.
Ora rappresentiamo il secondo membro dell’uguaglianza, 𝓒 A ∩ 𝓒 B, e verifichiamo che i due diagrammi coincidano. Come prima occorre graficare gli insiemi 𝓒 A e 𝓒 B rispettivamente:


e operando l’intersezione si ha l’insieme finale, il cui diagramma di Venn osserviamo essere uguale a quello dell’insieme 𝓒 (A U B):

poiché l’unione A U B è l’unico insieme a non essere colorato. Anche questa dimostrazione è così conclusa.
In alcuni libri di testo vengono raggruppate sotto il nome di leggi di De Morgan anche le seguenti uguaglianze:
A ∩ 𝓒 A = ∅
A U 𝓒 A = U
Di fatto, però, esse sono delle semplici proprietà dell’operazione complementazione. Suggeriamo di provare a verificarle usando i diagrammi di Venn per verificare di aver chiaro il metodo con cui procedere. In caso di dubbi o perplessità invitiamo a scrivere sul Forum.