Gli asintoti obliqui

Nell'ampio e variegato panorama dell'analisi matematica, gli asintoti obliqui occupano una posizione intrigante, offrendo una prospettiva unica sul comportamento limite delle funzioni. A differenza degli asintoti orizzontali e verticali, che rispecchiano tendenze orizzontali o verticali illimitate, gli asintoti obliqui (o asintoti inclinati) rappresentano linee rette di pendenza non zero verso le quali una funzione si avvicina indefinitamente all'infinito. Questa pagina è dedicata all'esplorazione degli asintoti obliqui, dal loro significato matematico alle tecniche per identificarli, fino alle loro applicazioni e implicazioni.

Che cosa sono gli asintoti obliqui?

Un asintoto obliquo è una linea retta di equazione y=mx+q, dove m e q sono costanti reali (con \(m\ne 0\)), che approssima il comportamento di una funzione f(x) per x che tende a \(\pm\infty\). La presenza di un asintoto obliquo indica che, mentre x diventa molto grande in valore assoluto, la distanza tra la funzione e la retta y=mx+q tende a zero.

Una retta di equazione y=mx+q (con \(m\ne 0\)) si dice asintoto obliquo per una funzione f(x) per \(x\to\infty\) quando:

\(\lim\limits_{x\to \infty}{\lvert f(x)-(mx+q)\rvert}=0\)

Più precisamente, se la condizione è soddisfatta solo per \(x\to -\infty\) allora y=mx+q è un asintoto obliquo sinistro, mentre se la condizione è soddisfatta solamente per \(x\to +\infty\), è un asintoto obliquo destro.

Teorema dell’esistenza dell’asintoto obliquo

Il teorema afferma che una retta di equazione y=mx+q (con \(m\ne 0\)) è un asintoto obliquo per una funzione f(x), se e solo se:

• \(\lim\limits_{x\to \infty}{\frac{f(x)}{x}}=m\)

• \(\lim\limits_{x\to \infty}{(f(x)-mx)}=q\)

Se tali condizioni sono soddisfatte, allora la retta y=mx+q è un asintoto obliquo per la funzione f(x). Se le condizioni sono soddisfatte solamente per \(x\to -\infty\) o \(x\to +\infty\), allora y=mx+q sarà solamente asintoto obliquo sinistro o destro, rispettivamente.

Esempio di asintoto obliquo

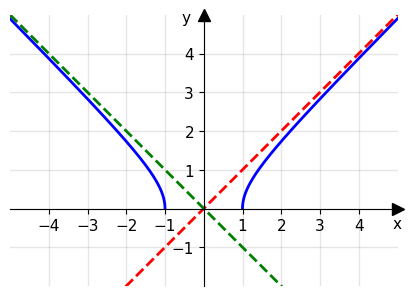
Consideriamo ad esempio la funzione \(f(x)=\sqrt{x^2-1}\). Per poter trovare eventuali asintoti obliquo per la funzione f(x), dobbiamo seguire le condizioni poste dal teorema precedente.

Verificando la prima condizione per \(x\to -\infty\), abbiamo che:

\(\lim\limits_{x\to -\infty}{\frac{\sqrt{x^2-1}}{x}}=\lim\limits_{x\to -\infty}{\frac{\lvert x\rvert\sqrt{1-\frac{1}{x^2}}}{x}}\)

e visto che \(\lvert x\rvert = -x\) per \(x\to -\infty\), otteniamo che:

\(\lim\limits_{x\to -\infty}{\frac{\sqrt{x^2-1}}{x}}=\lim\limits_{x\to -\infty}{\frac{\lvert x\rvert\sqrt{1-\frac{1}{x^2}}}{x}}=\lim\limits_{x\to -\infty}{\frac{-x}{x}}=m=-1\)

Allo stesso modo possiamo ottenere m per \(x\to +\infty\), infatti in questo caso \(\lvert x\rvert = x\) per \(x\to +\infty\), quindi otteniamo:

\(\lim\limits_{x\to +\infty}{\frac{\sqrt{x^2-1}}{x}}=\lim\limits_{x\to +\infty}{\frac{\lvert x\rvert\sqrt{1-\frac{1}{x^2}}}{x}}=\lim\limits_{x\to +\infty}{\frac{x}{x}}=m=1\)

A questo punto possiamo procedere con la seconda condizione del teorema:

\(\lim\limits_{x\to -\infty}{\sqrt{x^2-1} -(-1)x}=\lim\limits_{x\to -\infty}{\lvert x\rvert\sqrt{1-\frac{1}{x^2}} +x}=\lim\limits_{x\to -\infty}{-x+x}=q=0\)

Analogamente per \(x\to +\infty\):

\(\lim\limits_{x\to +\infty}{\sqrt{x^2-1} -x}=\lim\limits_{x\to +\infty}{\lvert x\rvert\sqrt{1-\frac{1}{x^2}} +x}=\lim\limits_{x\to +\infty}{x-x}=q=0\)

Questo significa che y=-x è asintoto obliquo sinistro per f(x), mentre y=x è asintoto destro per f(x).

Gli asintoti obliqui, con la loro capacità di catturare tendenze asintotiche non parallele agli assi, arricchiscono notevolmente la nostra comprensione delle funzioni matematiche e del loro comportamento limite. Attraverso lo studio di questi asintoti, siamo in grado di decifrare e visualizzare la complessità nascosta dietro le equazioni matematiche, aprendo nuove vie per l'applicazione della teoria dei limiti in contesti pratici e teorici.