Teorema dell’esistenza degli zeri

Nel cuore dell'analisi matematica si trova il teorema dell'esistenza degli zeri, un principio fondamentale che garantisce la presenza di almeno uno zero per una funzione continua in un intervallo chiuso e limitato, dato che la funzione assume valori di segno opposto alle estremità dell'intervallo.

Questo teorema, noto anche come teorema degli zeri, è un pilastro nell'ambito dello studio delle equazioni e delle funzioni, offrendo un ponte tra l'analisi pura e le sue applicazioni pratiche. Questa pagina mira a esplorare in dettaglio la natura, la dimostrazione e le implicazioni di questo teorema, illuminando il suo ruolo cruciale in vari campi della matematica.

Enunciato del teorema dell’esistenza degli zeri

Il teorema dell’esistenza degli zeri stabilisce che: sia f una funzione definita e continua su un intervallo chiuso e limitato [a,b]. Se \(f(a)\cdot f(b)<0\), allora esiste almeno un punto \(x_0 \in (a,b)\) tale che \(f(x_0)=0\).

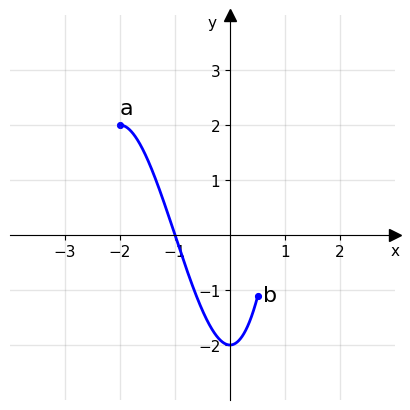
Nota: la condizione espressa del teorema è sufficiente, ma non necessaria. Infatti una funzione può ammettere degli zeri avendo anche i valori estremi non discordi.

Dimostrazione del teorema dell’esistenza degli zeri

La dimostrazione del teorema si basa sul concetto di continuità e sulla proprietà del valore intermedio. Senza entrare in una dimostrazione formale completa, l'idea chiave è che, poiché la funzione è continua e i valori alle estremità dell'intervallo hanno segni opposti, la funzione deve attraversare l'asse delle x (dove il valore della funzione è zero) almeno una volta mentre si passa da a a b.

Esempio applicazione del teorema dell’esistenza degli zeri

Consideriamo la funzione \(f(x)=x^2-4\) nell’intervallo chiuso e limitato [-3, 1]. Possiamo notare che \(f(-3)=5\) e \(f(1)=-3\), questo significa che \(f(-3)\cdot f(1) = 5\cdot(-3)=-15 <0\). Di conseguenza, per il teorema dell’esistenza degli zeri, la funzione f(x) ammette almeno uno zero nell’intervallo (-3, 1). Infatti, osservando il grafico della funzione nell’intervallo [-3,1], vediamo che la funzione interseca almeno una volta l’asse delle ascisse.

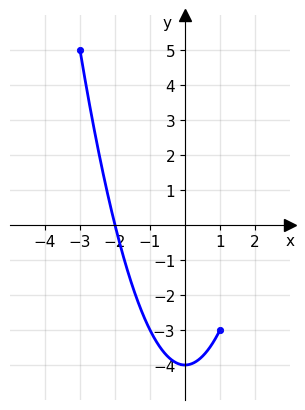
Importanza e applicazioni

Il teorema dell'esistenza degli zeri ha implicazioni profonde e applicazioni vastissime:

• Risoluzione di equazioni: Fornisce una base teorica per l'applicazione di metodi numerici, come il metodo di bisezione.
• Analisi matematica: È fondamentale nello studio delle proprietà delle funzioni continue, come l'esistenza di massimi e minimi.
• Fisica e ingegneria: Aiuta a determinare i punti di equilibrio in sistemi fisici e ingegneristici modellati da equazioni differenziali o algebriche.

Riflessioni finali

Attraverso l’applicazione del teorema dell'esistenza degli zeri , matematici, fisici, ingegneri e scienziati in vari campi possono ottenere intuizioni preziose sul comportamento dei sistemi che studiano, dimostrando ancora una volta come concetti matematici apparentemente astratti abbiano applicazioni concrete nel mondo reale.