Funzione continua e continuità

Nel cuore dell'analisi matematica, il concetto di continuità di una funzione rappresenta uno degli aspetti fondamentali che collegano insieme il calcolo differenziale, l'analisi dei limiti, e molte altre aree della matematica. La continuità di una funzione non solo rivela il comportamento fluido o ininterrotto di una funzione attraverso il suo dominio, ma offre anche una base per comprendere concetti più complessi come la derivabilità e l'integrazione. Esploriamo insieme la natura, l'importanza e le applicazioni della continuità nelle funzioni matematiche.

Funzione continua in un punto

Una funzione f(x) si dice continua in un punto \(x_0\) del suo dominio se soddisfa le seguenti condizioni:

• \(f(x_0)\) è definita, ovvero \(x_0\) fa parte del dominio di f.

• Il limite di f(x) per x che tende ad \(x_0\) esiste, è finito ed è uguale a \(f(x_0)\).

Matematicamente, sia \(f: \mathbb{R}\rightarrow\mathbb{R}\) una funzione reale di variabile reale e sia \(x_0 \in Dom(f)\) un punto di accumulazione di \(Dom(f)\). La funzione f si dice continua nel punto \(x_0\) quando 

\(lim_{x\to x_0^-} f(x)=lim_{x\to x_0^+} f(x)=lim_{x\to x_0} f(x)=f(x_0)\)

Nota: Si può dimostrare che tutte le funzioni elementari (funzione potenza, funzione valore assoluto, funzioni esponenziali e logaritmiche, funzioni goniometriche) sono continue nei punti dove sono definite.

Esempi di funzione continue

Di seguito vengono riportati alcuni esempi di funzioni continue:

• Consideriamo la funzione \(f(x)=x+1\), essa è continua in ogni punto appartenente al suo dominio. Per esempio è continua in \(x_0=1\):

  

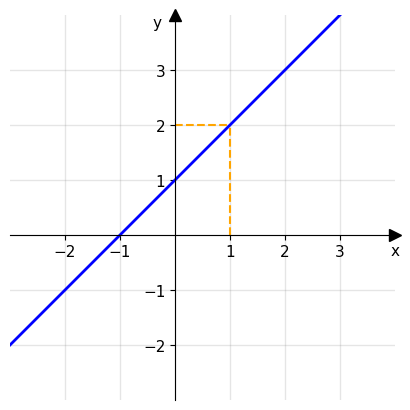
• Ora consideriamo la funzione \(f(x)=x^3\). Anche in questo caso la funzione è continua in ogni suo punto del suo dominio:

  

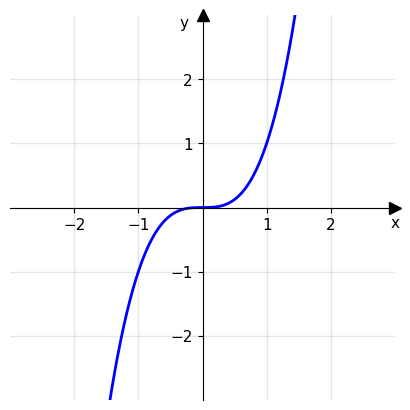
• La funzione sin(x) è continua in ogni punto appartenente al suo dominio:

  

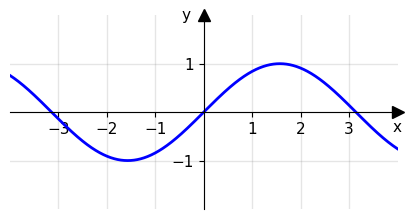
L'importanza della continuità

La continuità di una funzione in un punto o su un intervallo fornisce intuizioni fondamentali sul suo comportamento. Una funzione continua non presenta salti, discontinuità o asintoti nel suo grafico; il che significa che può essere disegnata senza sollevare la penna dal foglio. Questa proprietà è fondamentale per molteplici ragioni:

• Prevedibilità: Le funzioni continue offrono una certa prevedibilità nel loro comportamento, permettendo agli studiosi di matematica, fisica, ingegneria e altre discipline di modellare fenomeni naturali e processi con maggiore sicurezza.

• Analisi complessa: La continuità è una precondizione per la derivabilità. Una funzione deve essere continua in un punto per poter avere una derivata in quel punto, il che è cruciale nell'analisi dei tassi di cambiamento e nelle ottimizzazioni.

• Teoremi fondamentali: Numerosi teoremi dell'analisi matematica, come il Teorema del Valore Intermedio e il Teorema di Weierstrass sul valore estremo, presuppongono la continuità delle funzioni coinvolte.

Esempi e applicazioni

• Funzioni polinomiali: Tutte le funzioni polinomiali sono continue in tutto il loro dominio, che è l'insieme dei numeri reali. Questo le rende strumenti potenti per modellare una vasta gamma di fenomeni senza preoccuparsi di possibili discontinuità.

• Funzioni trigonometriche: Le funzioni trigonometriche come seno e coseno sono continue in tutto il loro dominio, rendendole indispensabili nell'analisi delle onde, nella fisica e in altri campi tecnici.

In conclusione, il concetto di continuità è uno dei pilastri su cui si fonda l'analisi matematica. Offre una lente attraverso cui possiamo esaminare e comprendere il comportamento delle funzioni matematiche, sia nelle loro manifestazioni teoriche che nelle applicazioni pratiche. Attraverso lo studio della continuità, possiamo avvicinarci al mondo complesso dei fenomeni naturali e delle costruzioni umane con gli strumenti della prevedibilità, dell'analisi e dell'ottimizzazione