Punti di discontinuità e punti singolari

Nell'universo dell'analisi matematica, il concetto di continuità e discontinuità di una funzione gioca un ruolo chiave nella comprensione del comportamento delle funzioni attraverso il loro dominio. I punti di discontinuità, in particolare i punti di singolarità, sono di grande interesse perché rappresentano le "rotture" o gli "interruttori" nel grafico di una funzione, dove il suo comportamento cambia in modo significativo. Questa pagina esplora i diversi tipi di punti di singolarità, le loro caratteristiche, e l'importanza di identificarli.

Punto singolare di una funzione

Data una funzione f reale ed un punto \(x_0 \in \mathbb{R}\), si dice che \(x_0\) è un punto singolare per f (oppure f presenta una singolarità in \(x_0\)) in ciascuno dei seguenti due casi:

• se il punto \(x_0\) appartiene al dominio della funzione, ma la funzione non è continua in \(x_0\).
• se il punto \(x_0\) non appartiene al dominio della funzione, ma è di accumulazione per esso.

Nota: Nel primo caso, ovvero se \(x_0\) appartiene al dominio della funzione, un punto singolare viene anche detto punto di discontinuità.

Che cos'è un punto di discontinuità?

Un punto di discontinuità in una funzione si verifica in un punto di accumulazione \(x_0\) appartenente al dominio, dove la funzione non è continua. Ciò significa che, in \(x_0\), la funzione può presentare un salto o un'altra forma di "interruzione" che impedisce di tracciare il grafico della funzione senza sollevare la penna dal foglio.

Esempi punti singolari e punti di discontinuità

Per comprendere meglio la distinzione tra punto di discontinuità e punto singolare, consideriamo i due seguenti esempi.

Consideriamo la funzione a tratti \(f(x)=\begin{cases}1 &x\ge 0 \\-1 &x <0\end{cases}\). Il punto x = 0 appartiene al dominio della funzione, infatti \(f(0)=1\), ma la funzione non è continua in esso visto che il limite destro e sinistro in 0 sono diversi tra di loro, di conseguenza \(lim_{x\to 0} f(x)\) non esiste. Questo significa che il punto x = 0 è un punto singolare o di discontinuità.

Mentre se consideriamo la stessa funzione a tratti, ma senza la condizione \(\ge 0\), \(f(x)=\begin{cases}1 &x> 0 \\-1 &x <0\end{cases}\) In questo caso il punto x = 0, non appartiene al dominio della funzione e la funzione non è continua, per lo stesso motivo di prima. La differenza sta nel fatto che il punto x = 0 è solamente un punto singolare.

Classificazione dei punti singolari

I punti singolari possono essere classificati in tre categorie principali, basandosi sulla natura del punto singolare e sul comportamento dei limiti della funzione in quei punti.

• Singolarità eliminabile: un punto \(x_0\) è detto una singolarità eliminabile per una funzione f quando il limite della funzione esiste finito, ma è diverso da \(f(x_0)\) (in questo caso si parla anche di punto di discontinuità) oppure f non è definita in \(x_0\).
  
  
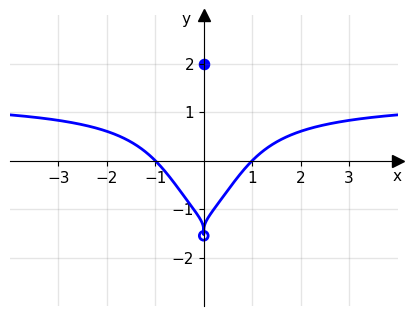
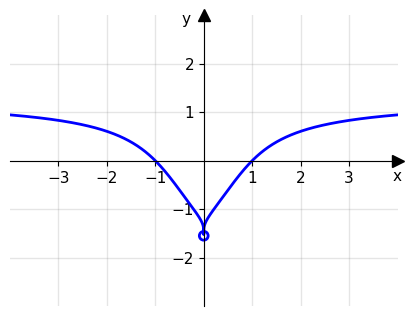
• Punto di salto: un punto \(x_0\) è detto un punto di salto (o singolarità di prima specie) per una funzione f se esistono limiti destro e sinistro in \(x_0\), ma sono diversi tra loro.
  
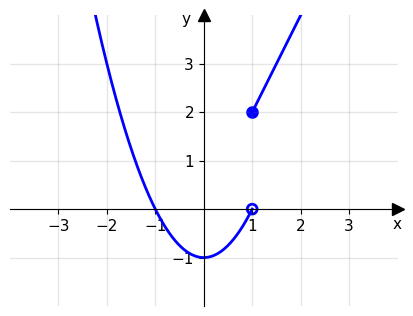
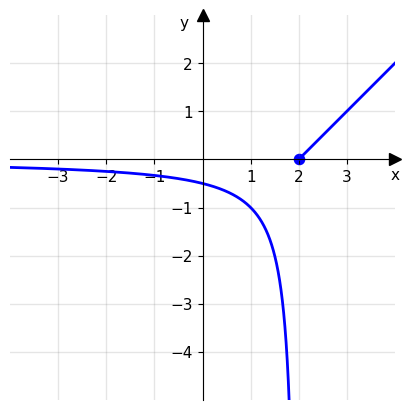
• Singolarità di seconda specie: un punto \(x_0\) è detto singolare di seconda specie se almeno uno dei due limiti (destro o sinistro) non esiste o è infinito.
  

Identificazione dei punti di singolarità

L'identificazione dei punti di singolarità in una funzione richiede l'analisi dei limiti e il calcolo diretto dei valori della funzione. Una strategia comune include:

• Calcolare i limiti destro e sinistro di f(x) in \(x_0\).
• Verificare il valore di \(f(x_0)\) se esiste.
• Confrontare i limiti con \(f(x_0)\)per determinare il tipo di discontinuità.

Conclusione

I punti di singolarità offrono una finestra sul comportamento complesso e variegato delle funzioni matematiche, rivelando le "crepe" e gli "interruttori" nel tessuto continuo delle loro rappresentazioni grafiche. La capacità di identificare, classificare e comprendere questi punti non solo arricchisce la nostra comprensione teorica delle funzioni ma apre anche la porta a applicazioni pratiche in campi che vanno dalla fisica all'ingegneria.