Limite finito per x che tende ad un valore finito

Il concetto di limite in matematica rappresenta uno dei pilastri fondamentali dell'analisi matematica e gioca un ruolo cruciale nello studio del comportamento delle funzioni. Quando parliamo del limite finito di una funzione per x che tende a un valore finito, ci riferiamo alla tendenza di una funzione ad avvicinarsi a un valore specifico mentre la variabile indipendente x si avvicina a un certo valore anch'esso finito. Questo concetto è essenziale per comprendere il comportamento delle funzioni nei punti di interesse e per l'applicazione di molti altri concetti matematici come la continuità, la derivabilità e l'integrabilità.

Definizione formale

Matematicamente, si dice che una funzione f(x) ha limite \(L\) per x che tende a \(x_0\) (dove \(x_0\) e \(L\) sono valori finiti), se per ogni numero \(\epsilon > 0\) esiste un numero \(\delta > 0\) tale che per ogni x nel dominio di f, se \(0<\lvert x-x_0\rvert < \delta\) allora \( \lvert f(x) - L \rvert < \epsilon\). In simboli:

\(\lim_{x\to x_0} f(x) = L\) se \(\forall \epsilon>0\;\exists\;\delta(\epsilon)>0\) t.c \(x \in Dom(f), 0<\lvert x-x_0\rvert < \delta \Longrightarrow \lvert f(x) - L \rvert < \epsilon\)

Questo significa che mentre x tende a x₀, la funzione converge al valore L.

Analisi della definizione di limite finito per x che tende ad un valore finito

La definizione può essere suddivisa in diverse parti per una comprensione più approfondita.

Partendo dalla parte di \(\forall \epsilon>0\): questa ci dice che per ogni valore positivo arbitrario di \(\epsilon\), per quanto piccolo possa essere, rappresenta una misura di quanto vicino vogliamo che f(x) sia ad L, sull’asse delle ordinate.

Dopo aver scelto un \(\epsilon\), la definizione afferma che possiamo trovare un numero \(\delta\), anch’esso positivo, che rappresenta una distanza intorno a x₀ sull’asse delle ascisse.

La parte \(0<\lvert x-x_0\rvert < \delta\) ci dice che stiamo considerando i valori di x che sono vicini a x₀. La disuguaglianza \(\lvert x-x_0\rvert < \delta\) significa che la distanza tra x e x₀ è meno di \(\delta\), ovvero, x è all’interno di un intervallo intorno a x0, ma non include x₀.

Questo implica che (\(\Longrightarrow \lvert f(x) - L \rvert < \epsilon\)) se abbiamo trovato un x che soddisfa la condizione precedente (cioè che x sia sufficientemente vicino ad x₀), allora il valore di f(x) sarà sufficientemente vicino a L. Più precisamente, la distanza tra f(x) e L sarà inferiore a \(\epsilon\).

Interpretazione grafica della definizione

Graficamente, questo concetto può essere rappresentato come l'avvicinamento della curva della funzione al valore L sull'asse delle ordinate mentre x si avvicina al valore x₀ sull'asse delle ascisse. Non è richiesto che la funzione assuma effettivamente il valore L quando x = x₀; ciò che conta è il comportamento di f(x) mentre x si avvicina a x₀.

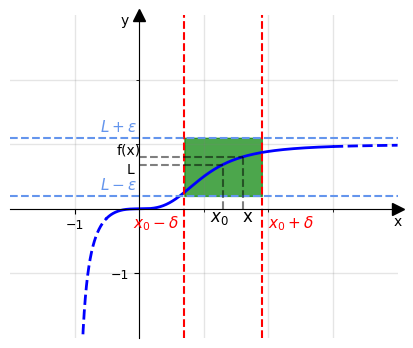
In particolare, la definizione di limite afferma che possiamo rendere la banda orizzontale stretta quanto vogliamo (rendendo \(\epsilon\) piccolo), e ci sarà sempre una banda verticale (determinata da \(\delta\)) tale che, quando x è dentro questa banda verticale (ma non uguale ad x₀), f(x) sarà all'interno della banda orizzontale.

Questa definizione formale cattura in modo rigoroso l'idea che f(x) si avvicina a L man mano che x si avvicina ad x₀. Non è necessario che f(x) sia uguale a L quando x = x₀ (infatti, f(x) potrebbe non essere definita per x = x₀), né è necessario che x raggiunga effettivamente x0.

Ciò che conta è che possiamo rendere f(x) arbitrariamente vicino a L semplicemente facendo in modo che x sia sufficientemente vicino ad x₀.

Nella pagina seguente verrà mostrato come avviene la verifica di un limite finito per x che tende ad un valore finito.