Teorema dell’esistenza del limite per funzioni monotone

Nell'ambito dell'analisi matematica, il concetto di funzioni monotone gioca un ruolo cruciale nello studio del comportamento delle funzioni e dei loro limiti. Le funzioni monotone, caratterizzate da una costanza nella direzione della loro crescita o decrescita, offrono una base solida per l'analisi dei limiti, facilitando la comprensione del comportamento asintotico delle funzioni in specifici intervalli o vicino a punti critici. Questa pagina esamina in modo dettagliato l'esistenza del limite per le funzioni monotone, mettendo in luce la loro importanza e applicabilità nell'analisi matematica.

Nota: una funzione f(x) si dice monotona su un intervallo del suo dominio, se è esclusivamente crescente o decrescente su quell’intervallo.

Enunciato teorema dell’esistenza del limite per funzioni monotone

Sia \(f:\mathbb{R}\rightarrow\mathbb{R}\) una funzione monotona nell’intervallo (a,b), abbiamo che:

• Se f è crescente su (a,b) ed \(x_0\in\mathbb{\bar{R}}\) è punto di accumulazione destro per (a,b), allora:

\(\exists\;\lim\limits_{x\to x_0^+} f(x) = \inf\limits_{x\in(a,b)} f(x)\)

• Se f è decrescente su (a,b) ed \(x_0\in\mathbb{\bar{R}}\) è punto di accumulazione destro per (a,b), allora:

\(\exists\;\lim\limits_{x\to x_0^+} f(x) = \sup\limits_{x\in(a,b)} f(x)\)

• Se f è crescente su (a,b) ed \(x_0\in\mathbb{\bar{R}}\) è punto di accumulazione sinistro per (a,b), allora:

\(\exists\;\lim\limits_{x\to x_0^-} f(x) = \sup\limits_{x\in(a,b)} f(x)\)

• Se f è decrescente su (a,b) ed \(x_0\in\mathbb{\bar{R}}\) è punto di accumulazione sinistro per (a,b), allora:

\(\exists\;\lim\limits_{x\to x_0^-} f(x) = \inf\limits_{x\in(a,b)} f(x)\)

Il teorema fondamentale che garantisce l'esistenza del limite per le funzioni monotone afferma che ogni funzione monotona limitata su un intervallo possiede limiti all'estremità di quell'intervallo. Questo teorema non solo stabilisce l'esistenza del limite, ma sottolinea anche la prevedibilità e la coerenza del comportamento delle funzioni monotone.

L'importanza di questo teorema risiede nella sua capacità di assicurare che, nonostante l'infinita varietà di comportamenti che una funzione matematica può esibire, le funzioni monotone mantengono una certa "disciplina" nel loro comportamento asintotico. Questo rende le funzioni monotone strumenti potenti nell'analisi dei limiti, specialmente in contesti dove altre tecniche possono risultare meno efficaci.

Esempio del teorema del limite di una funzione monotona

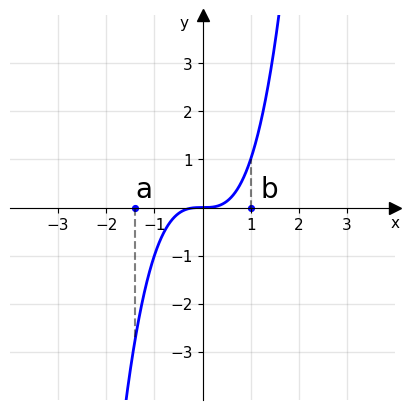
Consideriamo la funzione \(f(x)=x^3\) nell'intervallo (a,b), essa è una funzione monotona crescente. Questo significa che esistono:\(\lim\limits_{x\to a^+} x^3 = \inf\limits_{x\in(a,b)} x^3=f(a)\) e\(\lim\limits_{x\to b^-} x^3 = \inf\limits_{x\in(a,b)} x^3=f(b)\)

Considerazioni finali

L'esplorazione dell'esistenza dei limiti per funzioni monotone apre una finestra su uno degli aspetti più affascinanti dell'analisi matematica: la capacità di dedurre proprietà globali delle funzioni dal loro comportamento locale o dalla loro struttura intrinseca. Questo teorema non solo fornisce una garanzia teorica sull'esistenza dei limiti per un'ampia classe di funzioni, ma stimola anche ulteriori indagini sulle proprietà di tali funzioni e sui metodi per calcolare i limiti specifici.

In conclusione, il teorema dell'esistenza del limite per funzioni monotone si pone come un pilastro fondamentale nell'analisi matematica, evidenziando il legame intrinseco tra la struttura di una funzione e il suo comportamento asintotico.