Proprietà del prodotto cartesiano

Si consiglia di avere ben chiari il concetto di coppia ordinata (x,y) e la definizione di prodotto cartesiano spiegati ai link indicati. Tuttavia per comodità riprendiamo brevemente la definizione dell’operazione che andremo ad approfondire.

Dati due insiemi non vuoti A e B, l’insieme di tutte le coppie ordinate ottenute a partire dagli elementi di A e di B viene detto prodotto cartesiano di A per B (o di B per A):

A × B ≔ {(a,b) | a ∈ A, b ∈ B} oppure B × A ≔ {(b,a) | a ∈ A, b ∈ B}

con A × B ≠ B × A in generale, ossia l’operatore × di prodotto cartesiano tra due insiemi non è commutativo Inoltre l’operatore × non gode della proprietà associativa e ciò è evidente nell’esempio che segue.

Esempio 1: sia dato per semplicità il solo insieme A = {1} e si considerino i prodotti cartesiani A x (A x A) e (A x A) x A. Applicando la definizione di prodotto cartesiano otteniamo:

A x (A x A) = { ( 1,(1,1) ) } mentre (A x A) x A = { ( (1,1),1 ) }

e dato che le coppie devono rispettare un criterio di ordine si ha che i due insiemi non sono equivalenti, pur avendo gli stessi elementi nell’unica coppia ottenibile 1 e (1,1): A x (A x A) ≠ (A x A) x A.

Cardinalità del prodotto cartesiano

Ricordando il concetto di cardinalità di un insieme poniamo card(A) = n e card(B) = m con n, m ∈ ℕ o anche infiniti. Segue che la cardinalità, ovvero il numero di elementi presenti, dell’insieme prodotto cartesiano A x B (o B x A) è pari al prodotto degli elementi dei due insiemi tra i quali si esegue l’operazione:

card(A x B) = card(B x A) = card(A) ∙ card(B) = m∙n

con un numero di elementi infinito nel caso in cui almeno uno dei due insiemi abbia cardinalità infinita e l’altro non sia vuoto.

Esempio 1: dato A = {a | a ∈ ℕ}, B = {0,1} e C = {c | c ∈ ℕ \ {0}} si ha che la cardinalità dei vari insieme prodotto cartesiano è la stessa in tutte le combinazioni:

card(A x B) = card(A x C) = card(B x C) = ∞

e ciò deriva dal fatto che almeno uno degli insiemi nell’operazione di prodotto cartesiano ha sempre un numero infinito di elementi.

Distributività del prodotto cartesiano

Posto un insieme universo U e dati tre suoi sottoinsiemi generici A, B, C, per l’operazione di prodotto cartesiano valgono le seguenti proprietà di distribuzione:

• il prodotto cartesiano di un insieme rispetto all’intersezione di altri due insiemi è pari all’intersezione dei prodotti cartesiani tra il primo insieme e gli altri due, a due a due come segue:

  A x (B ∩ C)  = (A x B) ∩ (A x C)

• il prodotto cartesiano di un insieme rispetto all’unione di altri due insiemi è pari all’unione dei prodotti cartesiani tra il primo insieme e gli altri due, a due a due come segue: 

  A x (B U C)  = (A x B) U (A x C)

• il prodotto cartesiano di un insieme rispetto alla differenza di altri due insiemi è pari alla differenza dei prodotti cartesiani tra il primo insieme e gli altri due, a due a due come segue:

  A x (B\C) = (A x B) \ (A x C)

• la complementazione rispetto al prodotto cartesiano tra due insiemi è pari all’unione di tre prodotti cartesiani come segue:

   𝓒(A x B) = (𝓒A x 𝓒B) U (𝓒A x B) U (A x 𝓒B)

Nota: si ricordi che il prodotto cartesiano non è commutativo e occorre quindi prestare attenzione all’ordine dei termini per tutte le proprietà elencate.

Dimostrazione: proponiamo una verifica grafica simile a quella utilizzata per le leggi di De Morgan sfruttando la rappresentazione del prodotto cartesiano presentata insieme alla sua definizione. Qua ci limitiamo al caso dell’intersezione mentre le altre proprietà sono lasciate come esercizio; nel caso di dubbi nella loro dimostrazione suggeriamo di sfruttare il Forum.

Dati gli insiemi A, B, C ⊆ ℝ vogliamo dimostrare la veridicità della seguente uguaglianza:

A x (B ∩ C)  = (A x B) ∩ (A x C)

e poniamo come ipotesi A ≠ ∅ ⋀ B ∩ C ≠ ∅ (sottintendendo B ≠ ∅ ⋀ C ≠ ∅). Infatti se almeno una delle precedenti ipotesi è falsa, l’uguaglianza è banalmente verificata in quanto:

• nel caso A = ∅, tutti i prodotti cartesiani hanno come risultante ∅; 

• nel caso B ∩ C = ∅, il termine di sinistra nell’uguaglianza è banalmente ∅ e analogamente il termine di destra, in quanto intersezione tra due insiemi disgiunti (B e C).

Sotto queste ipotesi, che hanno il solo scopo di escludere casi banali ed evitare troppi grafici, procediamo graficando il primo membro dell’uguaglianza che coloriamo in giallo nel seguente piano cartesiano:

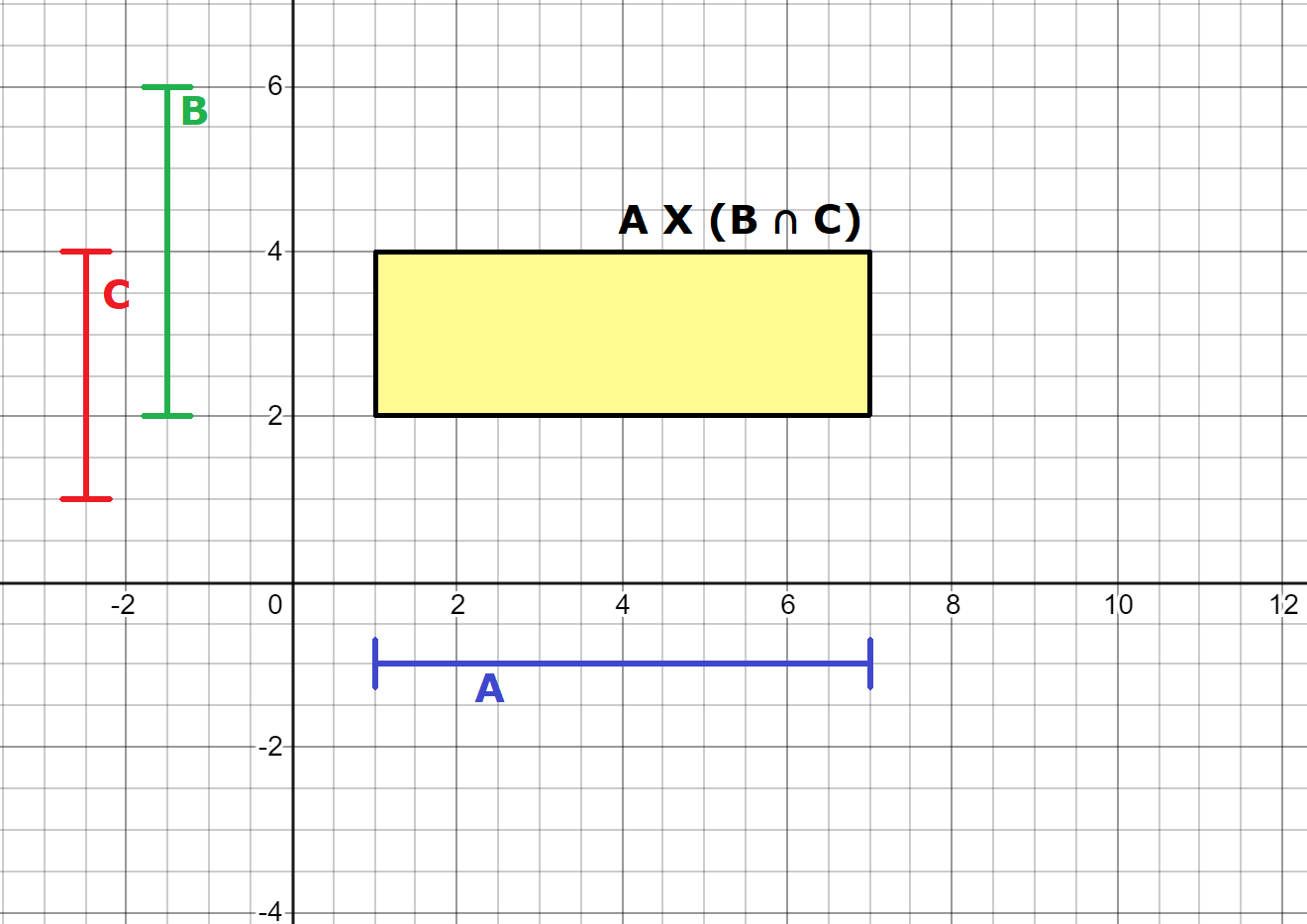
che otteniamo individuando ogni coppia ordinata con prima coordinata x ∈ A sull’asse delle ascisse e come seconda coordinata y ∈ (B ∩ C) sull’asse delle ordinate.

Ora non resta che graficare il secondo membro dell’uguaglianza e verificare che i due piani cartesiani coincidano. Procediamo graficando gli insiemi A x B e A x C rispettivamente in verde e rosso e poi ne prendiamo l’intersezione, in giallo:

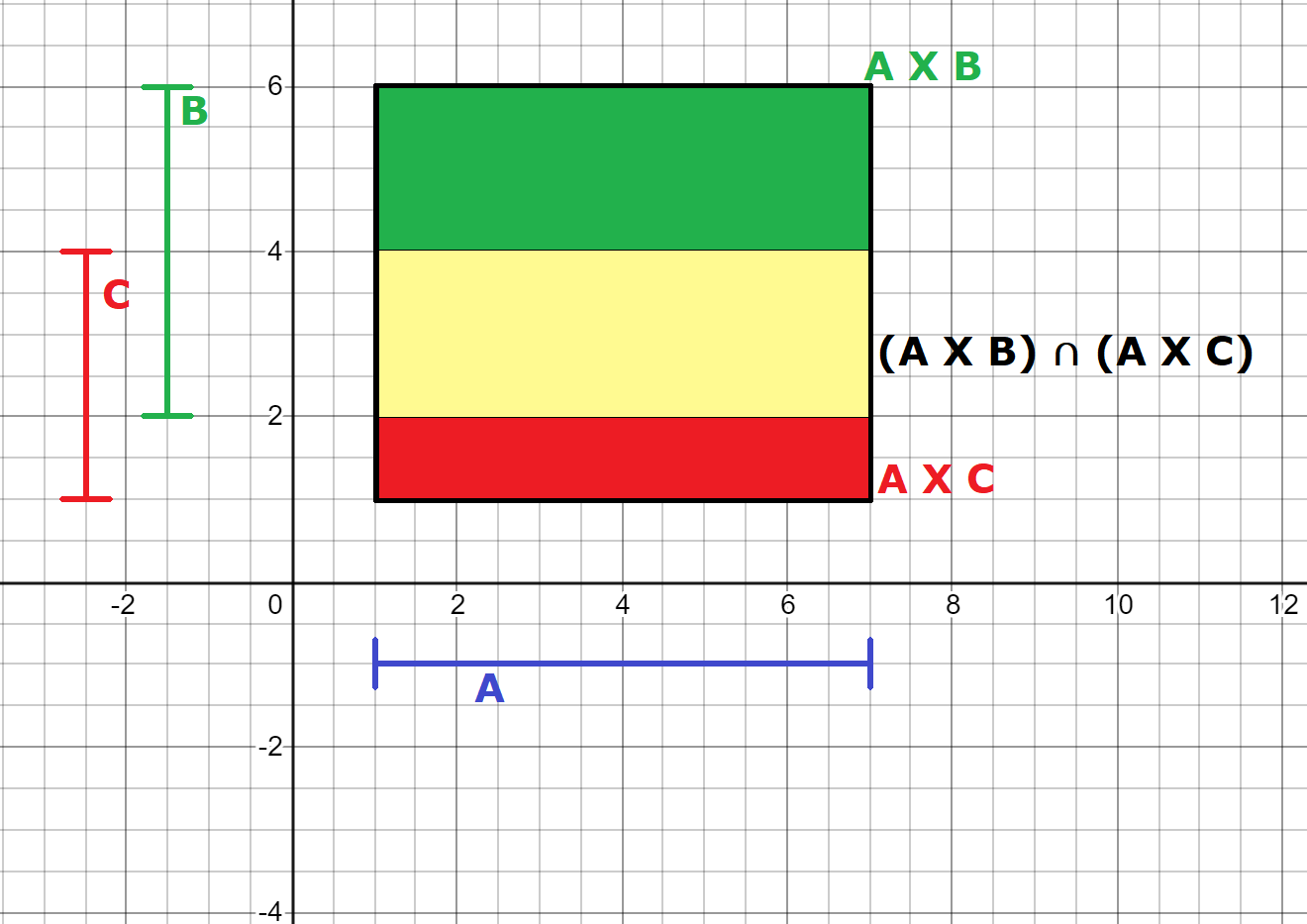
Osservando che i due insiemi "gialli" nei due piani cartesiani coincidono possiamo affermare che l’uguaglianza è dimostrata.

Per ulteriori approfondimenti, sono presenti proprietà del prodotto cartesiano meno comuni e di scarsa applicazione alla seguente pagina Wikipedia inglese.

Nota: Il concetto di prodotto cartesiano può essere esteso ad un caso più generale di n-uple ordinate (a₁,a₂,...,a_n) come elementi dell’insieme A₁ × A₂  × … × A_n con a_i ∈ A_i con i = 1,2,...,n.

Per tali n-uple valgono ancora le proprietà sopra elencate con opportuni accorgimenti.