Differenza simmetrica tra due insiemi

Avendo ben chiaro il concetto di insieme, sfruttando i diagrammi di Venn per visualizzare meglio le operazioni svolte e definendo un insieme universo U per evitare ambiguità, procediamo spiegando un’operazione insiemistica forse non così nota.

Dati A, B due insiemi generici contenuti in U, la differenza simmetrica di A e B restituisce un nuovo insieme risultante AΔB che è la classe di tutti gli oggetti del primo insieme (A) che contemporaneamente non appartengono al secondo insieme (B) unito alla classe di tutti gli oggetti del secondo insieme (B) che contemporaneamente non appartengono al primo insieme (A). L’insieme risultante, intuitivamente contenuto anch’esso in U, è definito come:

AΔB ≔ A\B U B\A ≔ {x ∈ U | (x ∈ A ⋀ x ∉ B) ⋀ (x ∈ B ⋀ x ∉ A) }

Un altro modo per descriverlo equivale a considerare l’unione dei due insiemi A e B a cui viene sottratta l’intersezione dei due, cioè gli elementi che appartengono ad entrambi gli insiemi, A ∩ B. In particolare nel caso di insiemi disgiunti, A ∩ B = ∅, la differenza simmetrica è equivalente all’unione.

La rappresentazione con il diagramma di Venn dell’insieme differenza simmetrica corrisponde alla parte colorata in arancione nella seguente figura:

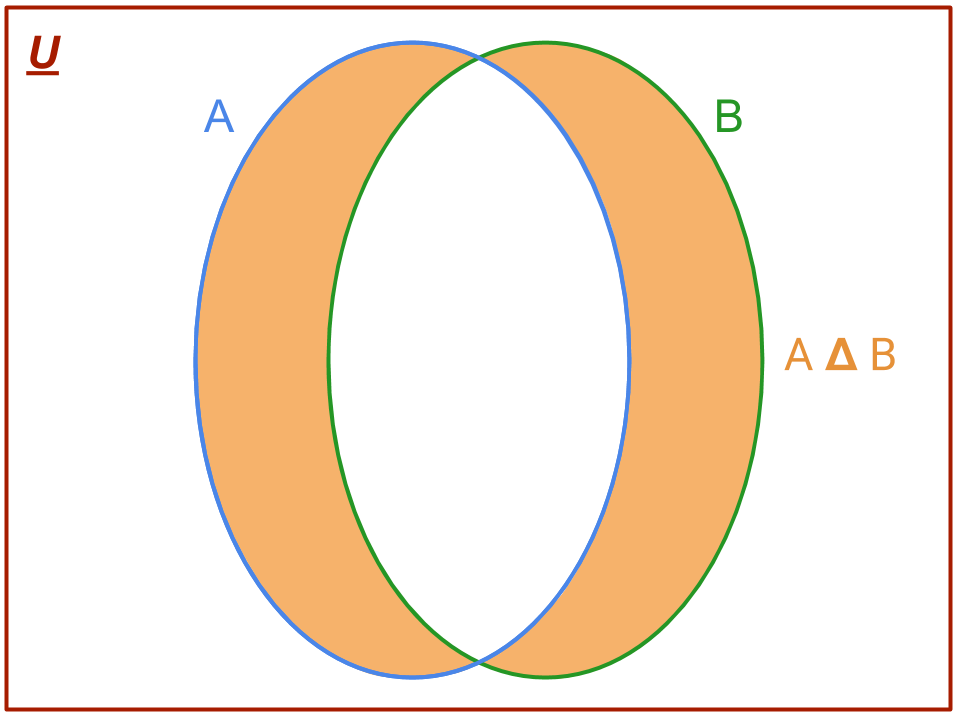
mentre per il caso particolare di insiemi disgiunti si ha:

Esempio 1: Sia U ≔ ℕ e siano A, B, C alcuni suoi sottoinsiemi definiti come A ≔ {1, 2, 3, 4}, B ≔ {3, 4, 5}, C ≔ {5, 6, 7}. Operando la differenza simmetrica tra i precedenti insiemi avremo

A Δ B = {1, 2, 5} 

A Δ C = {1, 2, 3, 4, 5, 6, 7}

B Δ C = {3, 4, 6, 7}

Un trucco per velocizzare i passaggi senza dover calcolare ogni volta i due insiemi differenza è quello di vedere gli elementi in comune e toglierli dall’unione dei due insiemi, in accordo con quanto detto sopra nella definizione.

Esempio 2: Sia U ≔ ℕ e siano A, B due suoi sottoinsiemi definiti come A ≔ {x ∈ U | x ≥ 4}, B ≔ {x ∈ U | x ≤ 4}. Operando la differenza simmetrica tra i precedenti insiemi avremo:

A Δ B =  {x ∈ U | x ≠ 4} = ℕ \ {4}

con particolare attenzione ai simboli di <, ≤, >, ≥. L’ultimo termine è una particolare notazione che sfrutta l’operazione di differenza per indicare l’insieme dei numeri naturali privato dell’elemento 4.

Proprietà della differenza simmetrica tra insiemi

Posto un insieme universo U e dati tre suoi sottoinsiemi generici A, B, C, per l’operazione di differenza simmetrica valgono le seguenti proprietà:

1. la differenza simmetrica di un insieme con sè stesso è l’insieme vuoto, posto B = A si ha:

   A Δ B = A Δ A = ∅ 

   poiché la differenza A \ A = ∅ come visto nella sua specifica lezione e l’unione di due insiemi vuoti è ancora un insieme vuoto;

2. la differenza simmetrica di un insieme con l’insieme vuoto ∅ è l’insieme di partenza, posto B = ∅ si ha

   A Δ B = A Δ ∅ = A 

   poiché le differenze A \ ∅ = A e ∅ \ A = ∅ come visto nella specifica lezione e l’unione A U ∅ = A come visto nella lezione sull’unione;

3. la differenza simmetrica di un insieme A con un suo sottoinsieme B è il complementare di B rispetto al contenitore A:

   A Δ B =  𝓒 B

   posto U ≔ A, poiché per ipotesi B ⊆ A e per definizione di sottoinsieme tutti gli elementi di B sono contenuti in A e quindi rimangono tutti gli elementi di Ache non appartengono ad B, ossia il complementare di B rispetto all’insieme contenitore A;

4. la differenza simmetrica di un insieme con l’insieme universo U è equivalente al complementare dell’insieme rispetto a U:

   A Δ U = 𝓒 A

   poiché per ipotesi A ⊆ U  e possiamo applicare la proprietà 3;

Nota: le precedenti 4 proprietà sono tutte casistiche particolari della proprietà n.3. In particolare si ricordi la nozione di sottoinsiemi impropri per la quale ∅, A ⊆ A.

• la differenza simmetrica di due insiemi disgiunti coincide con l’unione:

  A Δ B = A U B

  posto che A ∩ B = ∅, infatti non avendo nessun elemento comune le differenze A \ B = A e B \ A = B come visto per l’operazione di differenza e resta solo l’unione A U B;

• la differenza simmetrica è commutativa:

  A Δ B = B Δ A 

  poiché nella nozione di insieme non ha importanza l’ordine con cui vengono presi gli elementi;

• la differenza simmetrica è associativa:

  (A Δ B) Δ C = A Δ (B Δ C)

  sempre per il fatto che l’ordine dei termini non ha importanza;

• l’intersezione è distributiva rispetto alla differenza simmetrica:

  A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)

  e ciò è facilmente verificabile con dei diagrammi di Venn;

• la differenza simmetrica è transitiva:

  (A Δ B) Δ (B Δ C) = A Δ C

  e anche questo è facilmente verificabile con dei diagrammi di Venn.

Riassumiamo le 9 proprietà nella seguente tabella seguendo l’ordine precedente: